引言

现代战争中，战场具有不确定性、高机动性等特点，且作战地域通信基础设施薄弱，用户急需部署构设通信网络。移动Ad hoc网络因其对基础设施依赖度低、开设灵活、抗毁能力强、通信质量相对稳定可靠，在现代战争和商业中得到了大量运用[1]。移动Ad hoc网络是一种无预置基础设施的动态可重构无线网络，具备多个发送和接收功能的通信节点。网络中的节点既充当主机又充当路由器，通过一跳或多跳相互连接进行消息传输。在现代军事通信中，如何在野战条件下快速高效完成网络节点部署建立移动Ad hoc网络，是军事人员面临和亟待解决的难点问题[2-4]。

移动Ad hoc网络在美军历次作战行动中发挥着重要作用，受到了广泛关注。军用移动Ad hoc网络是在作战需求的主导下开设的，即通信的覆盖范围及通信地域形态由作战需求确定，故通信地域的范围大小和形态是随机的，具有多样性和不确定性。目前，在野战地域条件下，作战人员对通信网络（军用移动Ad hoc网络）的需求，包括通信质量良好、通信持续不间断、完全覆盖无死角等。同时，作为通信网络的规划建设人员，在给定通信地域后，如何使用最少的通信网络节点进行快速配置部署，才能使通信网络节点完成整个作战地域的全覆盖，保证该区域用户的通信需求，同时考虑降低成本、节约资源，这是通信规划建设人员面临的棘手问题。当前，移动Ad hoc网络的部署完成主要依托人员手工完成，设计速度慢、耗时长，无法对开设通信网络所需的设施设备数量提前进行预测规划，难以快速得出通信半径与所需节点数的内在关系，不能满足作战活动的实时、高效、准确、节约要求。

1 通信网络节点的部署配置

1.1 难以直接进行节点部署区域的分割方法

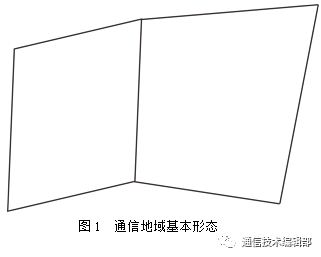
针对网络节点的部署，主要考虑以下问题。在作战地域确定后，即通信覆盖地域范围形态确定后，范围形态常常为三角形、规则多边形、不规则多边形等难以直接进行节点部署的形态，如图1所示。针对以上复杂形态直接进行节点部署，目前暂无较好的处理方法，属NP疑难问题。因此，需要对形态进行抽象分割，分割成易于处理的形态。

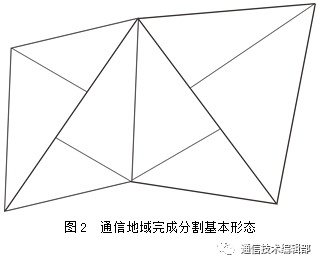
具体而言，对于难以直接开展节点部署的区域进行多次分割，分割为多个三角形，再对三角形做一条垂直于最大边的垂线（三角形的高），将其分割为两个直角三角形，以三角形的垂线为基线，分别在两个分割出的直角三角形内部进行节点部署（如图2所示）。对所有分割出的直角三角形完成节点部署后，即实现了整个区域的部署。

1.2 分割区域内部的节点部署分析

完成通信覆盖地域的直角三角形分割后，研究确定每个网络节点在三角形内部的具体排列部署方式，包括节点通信传输半径的选取、位置的确定等。节点部署的优劣主要由通信传输半径的选取和部署位置决定，其对部署工程量、资源消耗数量（节点设备数量、资金等）、完成任务时间等产生了重大影响。

节点在通信范围内发射消息，通常以圆形方式散播。因此，在节点部署上，可采用正方形、六边形等方式在直角三角形内部署节点[5]。本文将对不同部署方式的性能差异着重进行分析。R 为通信节点在保证通信质量的情况下传输信息的最大距离，r 为部署节点时根据需要选择的通信传输半径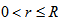（）。在r 时，可以获得较好的通信质量，实现区域内所有节点相互之间的不间断通信。在通信系统中，通信传输半径r 的大小可以在一定范围内调整，其与最少节点部署数量成反比关系。r 越大，需要的传输功率越大，所需节点数量越少；r 越小，需要的节点多，但通信传输半径r 大，要求发信设备功耗大，则设备续航时间短。这与野外战场条件低功耗的要求相矛盾，且不利于战场的隐蔽伪装。所以，节点通信传输半径的选择确定必须权衡设备功率与节点部署数量之间的关系。

在完成所有分割出的直角三角形的通信节点部署后，将所有节点累加即得到覆盖整个区域的最少节点数量。所以，关键在于怎么用最少节点部署实现直角三角形区域的完全覆盖，进而得出节点部署的最少数量和通信传输半径、直角边长度的关系。

2 节点部署算法

假设直角三角形的长为l 、宽为w ，节点部署的通信传输半径为r ，m(i) 表示与直角边l 平行的自下而上计数（计数基线为直角边l ）的第i 行节点数，i 表示行数。分别计算实现每一行区域完全覆盖的最少节点部署数量，再将各行节点数量求和，继而求得实现完全覆盖的最少节点总数。计算第1行节点数量时，以直角边的长度l 计算节点数量，这样可以确保区域完全覆盖。第i 行的节点数以连接三角形其余两边的第i 行（且平行于边l ）节点连线的长度计算，total 表示实现完全区域覆盖的最少节点总数。

2.1 使用正方形节点部署方式实现区域完全覆盖的最少节点算法

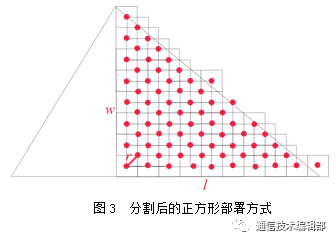
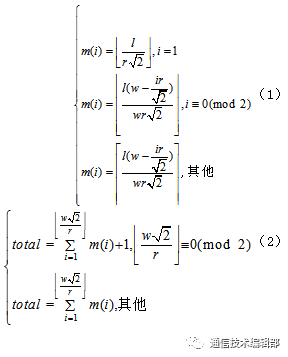
采用正方形方式部署节点时，从三角形底端紧贴高线位置部署第一个节点。第一个节点部署在正方形区域的中心位置，第二个节点部署在第一个节点覆盖的正方形区域的右上角，第三个节点部署在第二个节点覆盖的正方形的右下角。此外，根据这种模式部署其余节点。分割后的正方形部署方式，如图3所示。在计算部署节点数量时，要求部署节点的行数i 必须大于等于1。在满足该条件的情况下，首先计算覆盖第一行区域需要的节点数，再分别计算其余奇数行和偶数行需要的节点数，如式（1）所示；求和即得到所需节点总数total  ，如最大行数i 为偶数，需要增加一个节点，即总数  total加1，如式（2）所示。

当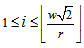时，有：

2.2 使用六边形节点部署方式实现区域完全覆盖的最少节点算法

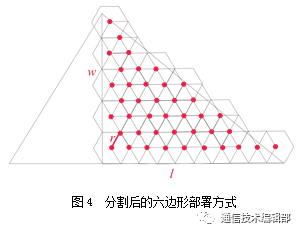
采用六边形方式部署节点时，从三角形底端紧贴高线位置部署第一个节点。第一个节点部署在六边形区域的中心位置，第二个节点部署在第一个节点覆盖的六边形区域的右上方，第三个节点部署在第二个节点覆盖的六边形区域右下方。同理，以此模式部署其余节点。分割后的六边形部署方式，如图4所示。在节点行数大于等于1的条件下，首先计算第一行的节点数，之后分别计算奇数行和偶数行的节点数，如式（3）所示；再进行求和，即得所需节点总数total ，如最大行数 为偶数时，则总数total 加1，如式（4）所示。

当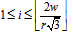时，有：

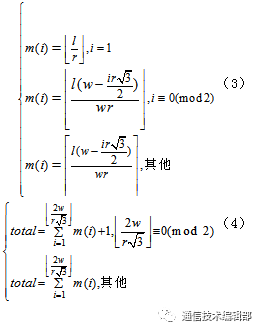
3 仿真分析

3.1 在直角三角形边长确定的情况下正方形和六边形部署方式所需最少节点数对比

当直角三角形边长已知，通信传输半径r 以间隔0.02 km在0.1～2.0 km变化时，对l 20 km＞ w=13 km，l=w=16km ，l=13km＜w=20km 这3种情形进行仿真，结果如图5所示。

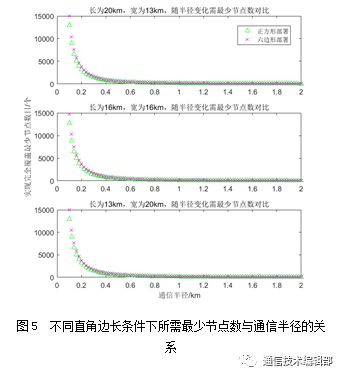
经对3种不同情形仿真可以看出，随着通信传输半径r 的增大，实现完全覆盖所需节点数逐渐减小。在通信传输半径r＜0.6km 时，两种部署方式所需的最少节点数数量较大，两种部署方式差距也较为明显；在部署半径r＞0.6km后，两者趋于平稳，且随着半径 的增大，所需节点数量不断减小。由此，在通信传输半径可以调节的情况下，r 的下界应选择0.6 km。同时，通过图形观察，r＞1.8km 后，所需节点数变化平缓。考虑发信功率等影响，r 应控制在0.6～1.8 km。此外可以看出，正方形部署方式优于六边形部署方式。为对两种部署方式进行定量比较，在每种情况下分别计算正方形和六边形部署方式在每个半径点处所需的最少节点数量，将不同部署方式在不同半径点处的所需节点数累加求差值，并与正方形部署的节点总数比较，得到3种情况下的六边形部署方式比正方形部署方式所需节点分别多出15.13%、15.10%、15.17%。可见，在区域内采用正方形部署方式效果更佳。

3.2 直角三角形面积确定，直角三角形两边长与最少节点数之间的关系

仿真中设置三角形面积为150 km2，假设直角三角形一边的长度以间隔0.5 km从2～300 km变化，通信传输半径分别设置为 r=0.6 km、1.0 km、1.5 km，仿真结果如图6所示。

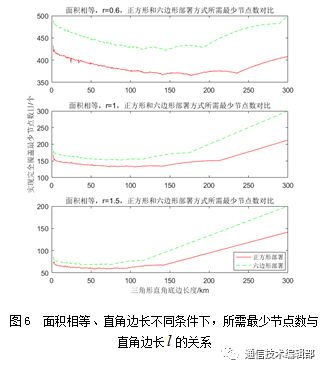
从仿真结果可以看出，正方形部署方式明显优于六边形部署方式，即在实际运用中，在发信设备通信传输半径相对固定、节点部署的面积范围大致相等的情况下，可以调整三角形两边的长度使所需节点数量最少。例如，从图6可以直接确定需节点最少的直角边长度，并确定所需的最少节点数量。可以看出，在通信半径不同时，所需节点数差距明显。在 r=0.6 km时，所需节点数远大于 r=1.5 km时的节点数量。在通信传输半径分别为 r=0.6 km、1.0 km、1.5 km时，对不同部署方式所需节点数求和计算比例差，得六边形部署方式比正方形部署分别多消耗17.26%、26.96%、33.37%的节点。同时，由图6得出，当直角边两边长度相近时，部署所需节点最少。

3.3 节点部署实际运用仿真

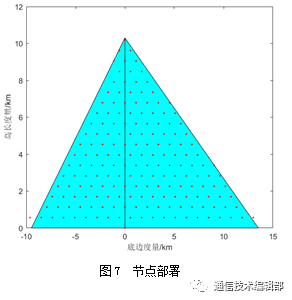
在将不便于直接部署节点的通信区域分割为直角三角形后，即在直角三角形边长和通信传输半径确定的情况下，可以实现节点的快速部署。实际作战行动中，可结合地图实现节点部署位置的精确定位，为节点部署节约成本和时间，大大提高效率。例如，三角形边长分别为23 km、17 km、14 km，通信半径选取0.8 km，则运用matlab程序对节点进行快速精确部署，如图7所示。由图7可知，该部署比手工配置部署效率大幅提升，同时验证仿真了实践结果与理论计算结果的一致性，符合预期。

4 结 语

为解决部分通信区域难以直接进行节点快速部署的问题，本文提出的区域分割方法能够有效处理该问题，通过定量对比不同节点部署方式，得出采用正方形部署效率更高的结论，平均比六边形部署方式节约15%的节点数量。对通信传输半径与节点部署数量之间的关系进行分析，同时考虑节点发射功率等因素，得出通信传输半径应控制在0.6～1.8 km，直角边两边长度应尽量相等等分析结果。为节点快速高效部署的实际运用提供了指导依据，并通过仿真实例进行了验证，大幅提高了节点部署效率。

参考文献：

[1] 郭嘉丰,张信明,谢飞等.基于节点空闲度的自适应移动Ad Hoc网络路由协议[J].软件学报,2005(05):960-969.

[2] 夏辉,贾智平,张志勇等.移动Ad Hoc网络中基于链路稳定性预测的组播路由协议[J].计算机学报,2013,36(05):926-936.

[3] 段淑敏,母军臣.进化计算的移动自组网服务节点部署算法研究[J].计算机仿真,2014,31(04):307-309,378.

[4] 徐伟强,汪亚明,俞成海等.移动Ad Hoc网络的跨层优化拥塞控制[J].软件学报,2010,21(07):1667-1678.

[5] Song R,Brown J D,Mason P C,et al.HMS: Holistic MPR Selection and Network Connectivity for Tactical Edge Networks[C].Military Communications Conference,2015:726-731.

作者：马建坤1，梁 涛2，王 海1，夏  志1

单位：1.陆军工程大学 通信工程学院，江苏 南京 210007；

2.南京电讯技术研究所，江苏 南京 210007

作者简介：马建坤，男，硕士，主要研究方向为电磁频谱管理；

梁 涛，男，博士，研究员，主要研究方向为通信抗干扰；

王 海，男，博士，教授，主要研究方向为宽带交换技术；

夏  志,男，硕士，主要研究方向为通信抗干扰。

本文刊登在《通信技术》2018年第4期

声明：本文来自通信技术编辑部，版权归作者所有。文章内容仅代表作者独立观点，不代表安全内参立场，转载目的在于传递更多信息。如有侵权，请联系 anquanneican@163.com。