基于秘密共享与同态加密的纵向联邦学习方案研究

作者简介

夏家骏

光之树（北京）科技有限公司算法工程师，主要从事纵向联邦学习的算法开发等工作。

鲁颖

光之树（北京）科技有限公司首席数据科学家，主要负责联邦学习整体算法框架研究等。

张子扬

光之树（北京）科技有限公司算法工程师，主要从事纵向联邦学习的算法开发等工作。

张钰婷

光之树（北京）科技有限公司助理工程师，主要从事纵向联邦学习的算法开发等工作。

张佳辰

光之树（北京）科技有限公司总经理及技术负责人，主要负责技术趋势研究等工作。

论文引用格式：

夏家骏, 鲁颖, 张子扬, 等. 基于秘密共享与同态加密的纵向联邦学习方案研究[J]. 信息通信技术与政策, 2021,47(6):19-26.

基于秘密共享与同态加密的纵向联邦学习方案研究

夏家骏 鲁颖 张子扬 张钰婷 张佳辰

（光之树（北京）科技有限公司，北京 100085）

摘要：由于日趋严格的隐私保护政策，各种隐私保护算法被提出。联邦学习能够在保护用户隐私不被泄露的情形下，运行各种机器学习算法。介绍了在不同场景下适用的联邦学习框架，并以逻辑回归为例介绍了纵向联邦学习的几种常用实现方式；此外，对各种实现方式的优缺点及适用场景进行了分析。

关键词：隐私计算；联邦学习；多方安全计算；同态加密；秘密共享

中图分类号：TP181 文献标识码：A

引用格式：夏家骏, 鲁颖, 张子扬, 等. 基于秘密共享与同态加密的纵向联邦学习方案研究[J]. 信息通信技术与政策, 2021,47(6):19-26.

doi：10.12267/j.issn.2096-5931.2021.06.003

0 引言

人工智能（Artificial Intelligence，AI）技术已经逐渐走进人们的生活，并应用于各个领域，它不仅给许多行业带来了巨大的经济效益，也为人们的生活带来了许多改变和便利。

一方面数据是AI的基石，数据能够为AI的发展提供丰富的数据积累和训练资源，随着大数据技术的突飞猛进，软硬件技术水平的不断提高，为人工智能取得重大突破提供了更多可能；另一方面，全球对于数据隐私方面的监管呈现全面化、密集化、严格化的趋势：我国自2018年以来，就有《科学数据管理办法》《国家健康医疗大数据标准、安全和服务管理办法（试行）》《中华人民共和国电子商务法》《数据安全管理办法（征求意见稿）》《个人金融信息（数据）保护试行办法》《关于规范银行与金融科技公司合作类业务及互联网保险业务的通知》等诸多国家法律、行政法规、部门规章等以保证数据隐私；与此同时，欧盟委员会开始强制实施《通用数据保护条例》（General Data Protection Regulation，GDPR），规定企业在对用户的数据收集、存储、保护和使用时的一系列行为规范^[1]。

联邦学习（Federated Learning，FL）由谷歌在2016年提出^[2]，并从此受到持续关注。在国内，“联邦学习”这一概念结合数据分布的具体场景，由微众银行率先将其分为横向联邦学习（Horizontal Federated Learning，HFL）、 纵向联邦学习（Vertical Federated Learning，VFL）与联邦迁移学习（Federated Transfer Learning，FTL）^[3]。联邦学习能够让多个参与方在满足用户隐私保护、数据安全和政府法规的要求下，进行数据使用和机器学习建模。本文介绍了在不同场景下适用的联邦学习方案，并以两方纵向联邦建立逻辑回归模型为例，介绍在隐私保护场景下的计算方案；然后，结合现有应用场景与平台框架，实现隐私保护场景下的两方联邦建模；最后，总结了各种方案的优缺点与适用场景。

1 联邦学习

联邦学习，通常用来描述两个或两个以上参与方共同参与，在保证各数据方的原始数据不出库的前提下，协作构建并使用机器学习模型的人工智能技术。联邦学习实际上是一个多学科融合的解决方案，包括但不限于机器学习、密码学、信息论、统计学等^[4]，其底层算子包括各种机器学习算法、同态加密、差分隐私、多方安全计算的各种协议（秘密共享、混淆电路、不经意传输、隐私保护集合求交）等。根据用于机器学习数据源在不同数据方之间的特征空间和样本空间的分布情况，联邦学习可以分为横向联邦学习、纵向联邦学习和联邦迁移学习，以下将对三者所对应的不同场景进行介绍（见图1）。

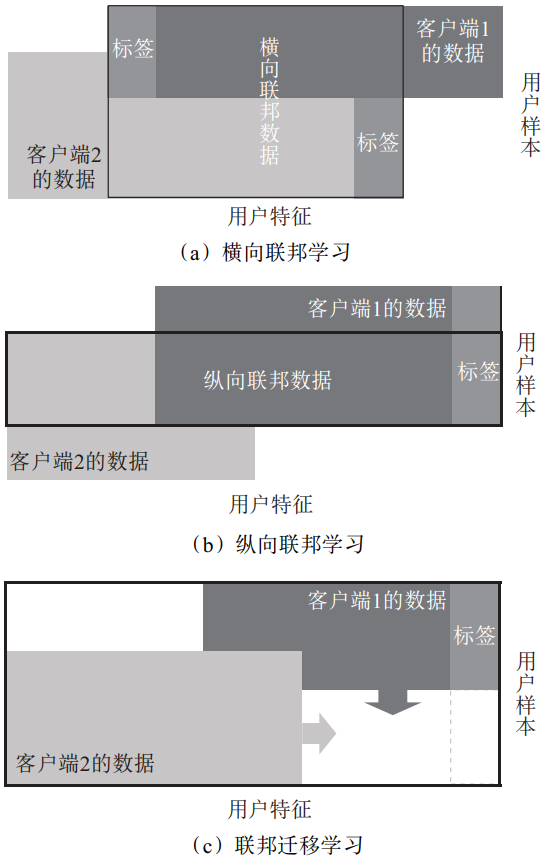
图1 联邦学习的分类

1.1 横向联邦学习

横向联邦学习对应的场景如下：在不同数据方之间，数据的特征空间比较相似，而样本空间很少重叠，即各数据方可以在相同的特征空间上用各方的所有样本来训练模型。一个经典的应用场景是：谷歌在其安卓手机自带的Gboard键盘上，使用横向联邦学习方法训练了机器学习模型，用以预测（联想）用户的下一个输入词 ^[5]。

横向联邦学习通常存在一个中心服务器，在每一轮（或几轮）的学习中，中心服务器将模型下发给各数据方，各数据方用本地数据训练出模型参数的更新梯度，服务器使用安全聚合（Secure Aggregation）方法将各方梯度收集到服务器端，计算出平均梯度，用以更新服务器端的模型，在下一轮下发给各数据方，直至收敛 ^[6]。FedSGD是谷歌最初提出的基于安全聚合方法的联邦平均随机梯度下降算法 ^[2]，此后为了减少通信开销，又提出了FedAvg算法，通过增加本地学习的轮数，减少了梯度聚合的交互次数，并且加速了模型收敛 ^[7]。此外，对于大量客户端同时训练的情形，同时引入了秘密共享机制，使某些客户端即使掉线，整个训练过程依然能够继续 ^[6]。

在某些情形下，中央服务器仍旧能够通过梯度信息反推训练集 ^[8]。因此，一个比较直观的解决方案是在训练聚合过程中增加差分隐私 ^[9]。而这将导致模型精度的损失，但在更大的程度上确保了数据安全。

1.2 纵向联邦学习

纵向联邦学习对应的是如下场景：在不同数据方之间，数据的样本空间有较大重叠，而特征空间不同，即各数据方可以使用相同样本的所有特征来训练模型。比如，基于用户画像建模时使用的特征，就可以不只局限于单来源的数据集，而是由相同用户的不同维度特征（如电商、通信、银行等数据）进行联合训练。在此情形下，各数据方分别拥有部分（与自身特征空间相关的）模型，因而模型的预测服务需要各方同时在线且授权才能完成。

与横向联邦学习架构不同的是，纵向联邦学习的过程可以在中心服务器的协调下完成，也可以在去中心化的情况下完成，因此中心服务器是非必须的。例如，在两方联邦学习的场景下，不需要存在一个可信第三方来协调双方的训练任务。

1.3 联邦迁移学习

联邦迁移学习对应的是如下场景：在不同的数据方之间，若数据的样本空间与特征空间均只有很少部分的重叠，则可以使用迁移学习的机制，即使用已有模型迁移到另一个样本空间进行训练。

迁移学习是常见的机器学习建模策略，在将现有模型应用到新的场景时，新场景的特征空间或者样本空间可能会发生变化，直接运用原来的模型将不能达到好的效果，因此需要通过原模型来辅助新的模型训练。联邦迁移学习，即在保护各方数据隐私的情况下，利用迁移学习的思想将知识迁移到新的环境中，从而在降低训练成本和标注成本的同时保证了隐私的安全性。与横向/纵向联邦学习不同，联邦迁移学习在参与各方的数据样本及特征均存在较小交集的情况下，可以利用其独特的训练模式，充分学习各方数据信息。例如，在金融场景中，可以利用大型金融企业的模型进行迁移学习，来提高小微企业的欺诈检测模型的效果。

联邦迁移学习通常将源领域样本的特征和目标领域的特征经过隐私转化后，通过加密算法和多方安全计算计算源领域样本与目标领域样本的关联程度，再以关联程度为权重将源领域样本的标签信息迁移到目标领域的样本。在安全性方面，联邦迁移学习采用同态加密及ABY等算法保证隐私安全，微众银行 ^[10]提出基于加法同态加密的模型训练和预测方法：各方在本地计算的中间数据，加密后发送给对方；接收方利用加密值计算对方的参数梯度，并加上随机数以掩盖梯度后发送给对方；各方解密后发送给对方以更新参数。此后，微众银行 ^[11]提出用SPDZ或ABY代替加法同态加密进行训练，在效率和安全性方面可以得到提升。

2 纵向联邦学习的实现方式

本节将以纵向两方逻辑回归模型为例，介绍在纵向数据分布中，隐私保护算法的实现方式。首先介绍逻辑回归模型的子模型拆分方式，然后对基于同态加密以及基于秘密共享的两种隐私保护逻辑回归模型训练方法进行研究，最后比较两种方法的优缺点，并介绍其适用场景。

2.1 纵向逻辑回归子模型

以两方逻辑回归模型为例，假设双方分别为A、B，其中A方拥有特征x _A，B方拥有特征x _B与标签y（为简化后续计算，不妨假设y取值范围为{-1，1}，若y取值范围为{0，1}可通过线性函数映射，不影响结论）。假设逻辑回归模型参数为θ，显然可令h(x)= θ ^Tx = θ ^T_Ax _A+θ ^T_Bx _B，则逻辑回归的输出值为p(x)=1/1+e ^-h(x)。基于极大似然估计，目标函数为最小化-∏ _ip(y _ix _i) = -∏ _i1/1+e ^-h(yixi)，对其求对数不影响单调性，即为最小化∑ _ilog（1+e ^-h(yixi)），由于后续的隐私保护方式通常为密码学原语（秘密共享或同态加密），不支持指数对数计算，因此对此目标函数进行二阶泰勒展开，得：

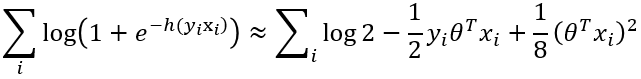
不妨令 u _i= θ ^Tx _i= θ ^T_Ax _Ai+θ ^T_Bx _Bi，即：

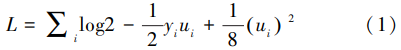
因此，对A、B双方来说，其本地子模型参数的梯度即为：

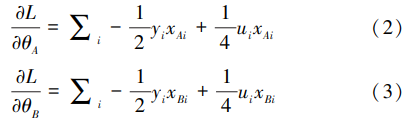
在纵向联邦学习的计算中，只要能够安全计算出公式(1)(2)(3)，就能够完成模型的训练。

2.2 基于同态加密的逻辑回归模型

逻辑回归模型训练过程只需要计算出公式(1)(2)(3)，更进一步，如果计算损失函数非必要的话，只需要计算公式(2)(3) 即可计算得出梯度，并能随之应用各种基于梯度（一阶导数）的优化方法。

2.2.1 同态加密

同态加密 ^[12]是一类特殊的加密方法，明文通过同态加密方法得到密文后，可实现密文间的计算（密文计算后解密的结果等价于明文计算的结果）。如果对密文进行加法（或乘法）运算后解密，与明文进行加法（或乘法）运算，结果相等，则称这种加密算法为加法（乘法）同态。如果同时满足加法和乘法同态，则称为全同态加密。然而，由于全同态加密的计算量太大，过于复杂，在实际应用中，加法同态加密通常便可满足需求，如Paillier加密。本文所用的同态加密即为Paillier加密，其满足密文的加法、数乘与明文一致。

2.2.2 基于Paillier加密的隐私保护两方纵向逻辑回归训练过程

图2给出了一种基于同态加密的隐私保护计算方法，其具体流程如下。

图2 一种基于同态加密的隐私保护两方纵向逻辑回归训练过程

（1）双方互相生成同态加密的公私钥对（pk _A，sk _A）及（pk _B，sk _B），并交换公钥pk _A，pk _B。

（2）无标签方A计算u _Ai及（u _Ai） ²，并将其使用自身公钥pk _A加密，发送给B；有标签方B计算1/4u _Bi-1/2y _i，并使用自身公钥pk _B加密，发送给A。

（3）A基于收到的[1/4u _iB-1/2y _i] _pkB，与自有数据u _Ai及x _Ai（通过 pk _B加密），可计算得密文[∂L/∂θ _A] _pkB，同时A生成随机掩码m _A，将[∂L/∂θ _A+m _A] _pkB发送给B；类似的，B计算出[∂L/∂θ _B+m _B] _pkA发送给 A，作为标签方，B可通过式（1）计算出[L] _pkA并发送给A。

（4）A用私钥sk _A解密出∂L/∂θ _B+m _B与L并发送给B，B用私钥sk _B解密出∂L/∂θ _A+m _A发送给A。

（5）A去除掩码获得∂L/∂θ _A，B去除掩码获得∂L/∂θ _B，双方基于梯度更新本地模型。

通过上述流程，可以在保护隐私的情形下完成双方的梯度计算、模型更新与损失函数计算。

2.3 基于秘密共享的逻辑回归模型

2.3.1 加法秘密共享

密码学（Cryptography）是建立在严格的数学定义、计算复杂度假设和证明基础之上的，其中多方安全计算（Multi-Party Computation，MPC）方向是专门研究多个参与方如何正确、安全地进行联合计算的子领域，而秘密共享则是多方安全计算中的重要领域（还有混淆电路等）。在加法秘密共享中，数据拥有者将数据x共享给两方A、B，两个秘密份额分别记作〈x〉 ^A，〈x〉 ^B，且x=〈x〉^A+〈x〉^B。

不妨令A方拥有x ₀，B方拥有x ₁，流程如下：

可以看到，在秘密共享的场景下，可以将明文的计算转化成秘密份额的计算，完成整个隐私保护计算任务。

2.3.2 基于加法秘密共享的隐私保护两方纵向逻辑回

图3给出了一种基于加法秘密共享的隐私保护计算方法，其具体流程如下。

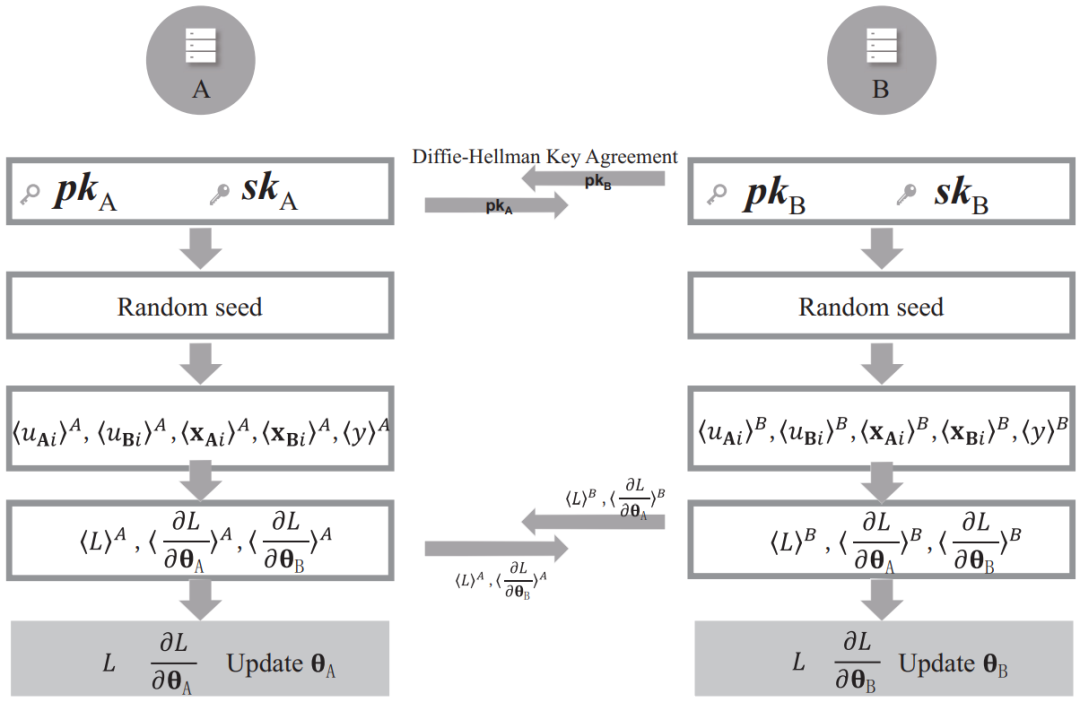
图3 一种基于加法秘密共享的隐私保护两方纵向逻辑回归训练过程

（1）双方协调随机数生成方式，确定伪随机数生成种子及双方数据维度。

（2）无标签方A计算u _Ai，并将其减去随机数r _uAi作为本地秘密〈u _Ai〉 ^A，而随机数r _uAi即为B方的秘密份额〈u _Ai〉 ^B；同时，将本地数据x _Ai减去随机数r _xAi作为本地秘密〈x _Ai〉 ^A，随机数r _xAi为B方的秘密份额〈x _Ai〉 ^B；相应的，有标签方B计算 u _Bi，并将其减去随机数r _uBi作为本地秘密〈u _Bi〉 ^B，而随机数 r _uBi 即为A方的秘密份额〈u _Bi〉 ^A；同时，将本地数据x _Bi减去随机数r _xBi作为本地秘密〈x _Bi〉 ^B，随机数r _xBi为A方的秘密份额〈x _Bi〉 ^A，对标签y也做相同操作，记作〈y〉 ^A和〈y〉 ^B。

（3）由于双方随机数生成方式相同，此时可认为A方拥有〈u _Ai〉 ^A，〈u _Bi〉 ^A，〈x _Ai〉 ^A，〈x _Bi〉 ^A，〈y〉 ^A，B方拥有〈u _Ai〉 ^B，〈u _Bi〉 ^B，〈x _Ai〉 ^B，〈x _Bi〉 ^B，〈y〉 ^B。因此，可分别计算得〈u _i〉 ^A= 〈u _Ai〉 ^A+〈u _Bi〉 ^A,〈u _i〉 ^B= 〈u _Ai〉 ^B+〈u _Bi〉 ^B，并各自使用秘密份额计算式（1）（2）（3）。得到 ^：

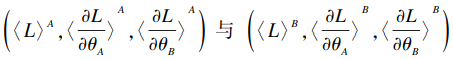
A将〈L〉 ^A,〈∂L/∂θ _B〉 ^A发送给B，B将〈L〉 ^B,〈∂L/∂θ _A〉 ^B发送给A，则双方可打开秘密获得自身梯度与共同的损失函数值。

（4）双方基于梯度更新本地模型。

3 隐私保护场景下的两方联邦建模场景

图4为一个完整的两方纵向联邦学习建模流程图。如某保险公司希望能够与某金融机构联合建立保险关注度模型，用以预测后续客户购买保险的意愿和能力，考虑到用户购买保险的能力也与其消费水平和收入水平相关，因此可以使用金融机构的一些数据。

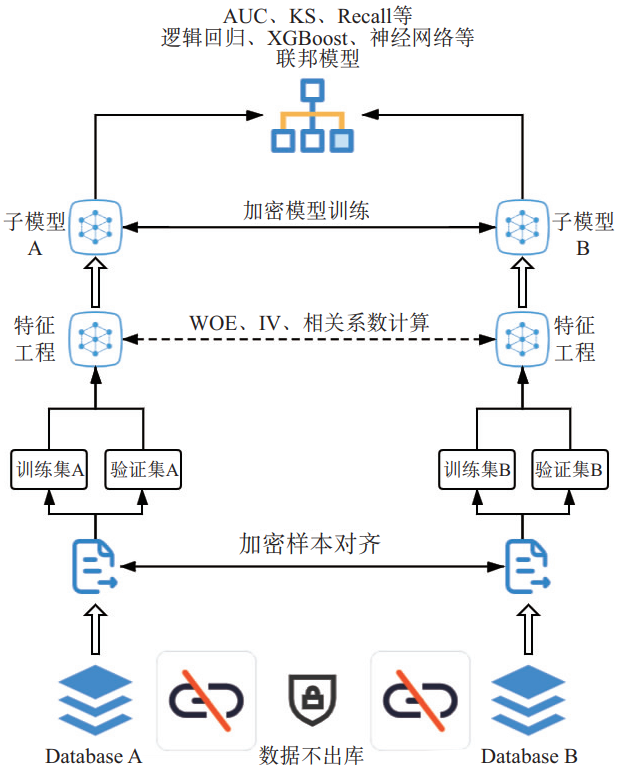
图4 联邦学习建模流程图

（1）消费信息：月线上线下消费金额、POS消费金额；消费笔数、消费金额区间、分布；日常购物消费金额、批发购物消费金额、娱乐消费金额、居住消费、是否奢侈品购物居多。

（2）投资理财信息：金融消费、理财投资偏好、贷款状态；房产状态、房产投资偏好等。

保险购买意向预测模型即可使用表1所述各类数据建立。

表1 建立保险购买意愿模型所用各方数据

“云间联邦学习平台”可用以进行多方的联邦学习任务，整个联邦学习系统框架如图5所示。在此场景中，可以选用两种技术路线，两者优缺点如下。

图5 云间联邦学习系统架构图

（1）联邦学习的时间可粗略分为计算时间与通信时间，一方面对于计算时间来说，秘密共享方案计算的加法即为密文的加法（加法同态一般是密文乘法），乘法即为密文的乘法（加法同态的数乘一般是密文的模幂），而且由于秘密共享方案的安全性是信息论安全性（Information-Theoretic Security）而非同态加密方案的计算安全性（Computational Security），其使用大整数主要用来确保对于浮点数类型转换后的精度问题。因此，在相同精度要求的情况下，秘密共享使用的有限域（通常如p=2 ¹²⁷-1或p=2 ⁶³-1）远小于同态加密（如2048 bit的Paillier加密，其N ²~2 ⁴⁰⁹⁶），因而其计算量也比同态加密所需的计算量减少很多。所以，秘密共享方案在计算速度上远快于同态加密运算;另一方面，对于通信耗时来说，秘密共享方案在计算乘法时，需要在各方之间交互大量数据（与参与训练的数据量相等），因此其在计算过程中也会对带宽造成很大压力，相比同态加密方案花费更长时间；此外，若计算任务开始前未生成足够的 Beaver’s Triplet，在计算阶段在线生成也将带来更多的耗时。

（2）对于同态加密方案，由于其每个明文加法在密文运算中都变成了大整数乘法，而数乘则变成了大整数在有限域的幂运算，通常来说，其密文计算时间是明文直接运算的200 倍（相同硬件条件下）以上；然而，其各方交互的是密文中间结果，这意味着随着数据集特征数的增加，交互传输的数据量基本不变；在非局域网/专线的环境下，通信对网络带宽的压力更小。此外，云间联邦学习平台对于Paillier加密算法支持GPU与FPGA加速，计算效率相比CPU提升5倍以上；并有相应的压缩算法减少Paillier密文的数据传输量，传输数据量压缩至约1/5，提高了传输效率。

（3）对于秘密共享方案，通常Beaver’s Triplet生成依赖于不经意传输协议或同态加密，因此其所需计算量并不低于同态加密且存在大量的数据传输；然而，这一过程独立于计算任务，因此参照SPDZ框架的做法，可以在计算任务执行前，各方预先生成足够的Beaver’s Triplet用于后续计算。若存在可信第三方协助（如央行或政府背书的其他部门），则也能够大大缩短这一时间并减少数据的吞吐量。此外，传统秘密共享方案需要秘密拥有者将自身秘密（数据）计算拆分成多个子秘密并发送给其他参与方，这一过程会带来很大的带宽压力；在光之树的云间联邦学习平台中，这一过程可以按数据拥有者的偏好选择拆分秘密，或DH密钥交换协议配合伪随机数生成器使各方生成相同的随机数，作为非秘密拥有者所获得的子秘密，而秘密拥有者只需要减去这些随机数即可得到其自身子秘密值。后者可将前者的大量数据通信过程减少到一次简单的密钥交换过程。

若存在可信第三方支持的情况下，或网络带宽较优时，秘密共享方案不失为一个更快的选择；而在网络环境较差时（如带宽受限的公网环境），同态加密方案则能通过缩短通信时间来弥补其计算量较大带来的不足。

4 结束语

本文介绍了联邦学习的各种场景，并以纵向场景中的逻辑回归模型为例，介绍了基于多方安全计算与同态加密两种技术路线的实现方案。总体来说，秘密共享方案更直观，运算更快，但其离线过程较复杂，会需要更多的离线时间，且在线训练时对网络传输的带宽要求较高；而同态加密方案的运算比较复杂，但其传输的数据量较少。所以，对于各种不同的场景，可以使用不同的方案，以达到效率的最优。

参考文献

[1] General. Data protection regulation[EB/OL]. (2018)[2021-03-20]. https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri =CELEX:32016R0679.

[2] Mcmahan H B, Moore E, Ramage D, et al.Federatedlearning of deep networks using model averaging[C]. Proceedings of the 20 th International Conference on Artificial Intelligence and Statistics ( AISTATS ),2017.

[3] YANG Q, LIU Y, CHEN T, et al. Federated machine learning: conceptand applications[C]. arXiv, 2019:1902. 04885.

[4] Kairouz P, McMahan H B, Avent B, et al. Advances and openproblems in federated learning[C]. ACM Transactions on Intelligent Systems and Technology(TIST), 2019(12).

[5] Hard A, Rao K, Mathews R, et al. Federated learning for mobile keyboardprediction[C]. arXiv, 2018: 1811.03604.

[6] Bonawitz Keith, Ivanov Vladimir, Kreuter Ben, et al.Practicalsecure aggregation for privacy-preserving machine learning[C]. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security (CCS’17). Association for Computing Machinery, New York, NY, USA, 2017:1175–1191.

[7] McMahan H B, Moore E, Ramage D, et al. Communication-efficient learning of deep networks from decentralizeddata[C], Proceedings of the 20th International Conference on ArtificialIntelligence and Statistics, AISTATS, 2017.

[8] YIN Hongxu, Arun Mallya, Arash Vahdat, et al. See through gradients: image batch recovery via gradInversion[C]. arXiv preprint arXiv, 2021:07586.

[9] Wei K, Li J, Ding M, et al. Federated learning with differential privacy: algorithms and performance analysis[C], IEEE Transactions on Information Forensics and Security, 2020(15): 3454-3469.

[10] Yang L, Chen T, Qiang Y. Secure federated transfer learning[C], ArXiv, abs/1812.03337.

[11] Sharma S, Chaoping X, Liu Y, et al. Secure and efficient federated transfer learning[C]//2019 IEEE International Conference on Big Data, 2569-2576.

[12] Paillier P. Public-key cryptosystems based on composite degree residuosity classes[C]. Proc EUROCRYPT"99, Czech Republic, 1999.

[13] Beaver D. Efficient Multiparty Protocols Using Circuit Randomization[C]//Advances in CryptologyCRYPTO"91, 11th Annual International Cryptology Conference, 1991(8):11-15.

Research on vertical federated learning based on secret sharing and homomorphic encryption

XIA Jiajun, LU Ying, ZHANG Ziyang, ZHANG Yuting, ZHANG Jiachen

(Points (Beijing) Technology Co., Ltd., Beijing 100085, China)

Abstract: Due to the promulgation of more and more privacy protection policies, many privacy preserving computing algorithms are developed. Among them, federated learning is practical in building machine learning algorithms under privacy preserving computing. This article, introduces different federated learning frameworks for different datapartition case, and demonstrates vertical federated learning with logistic regression as an example. Finally, it introduces the pros and cons of different implementations and their applicable scene.

Keywords: privacy preserving computing; federated learning; multi-party computation; homomorphic encryption; secret sharing

本文刊于《信息通信技术与政策》2021年 第6期

声明：本文来自信息通信技术与政策，版权归作者所有。文章内容仅代表作者独立观点，不代表安全内参立场，转载目的在于传递更多信息。如有侵权，请联系 anquanneican@163.com。