比利时鲁汶大学(KU Leuven)的研究人员发表了一篇初步论文[1],通过一个名为Magma的程序,在62分钟的时间内,使用单核处理器,完成了安全级别为level 1的SIKEp434的有效密钥恢复攻击。对于具有更高安全级别的SIKEp503 (level 2)、SIKEp610 (level 3)和SIKEp751 (level 5),分别在2小时19分钟、8小时15分钟和21小时37分钟内被破解。
SIKE是一种基于超奇异同源的密钥封装(KEM)算法,目前已经进入NIST后量子密码标准化的第四轮候选名单。通常来说,这些缺陷可以通过对算法进行小的修改来解决。但如果无法修复,那么SIKE算法将从后量子密码标准化的进一步考虑中被放弃。

01 SIKE和SIDH
说到SIKE就不得不说到它背后的协议——超奇异同源Diffie-Hellman (SIDH)。
SIDH最早于2011年[2]提出,作者从超奇异椭圆曲线同源的角度提出了一种抵抗量子攻击的密码系统,该密码依赖于计算超奇异椭圆曲线间同源的困难性问题。而且密钥长度明显地要比其他后量子密码短。
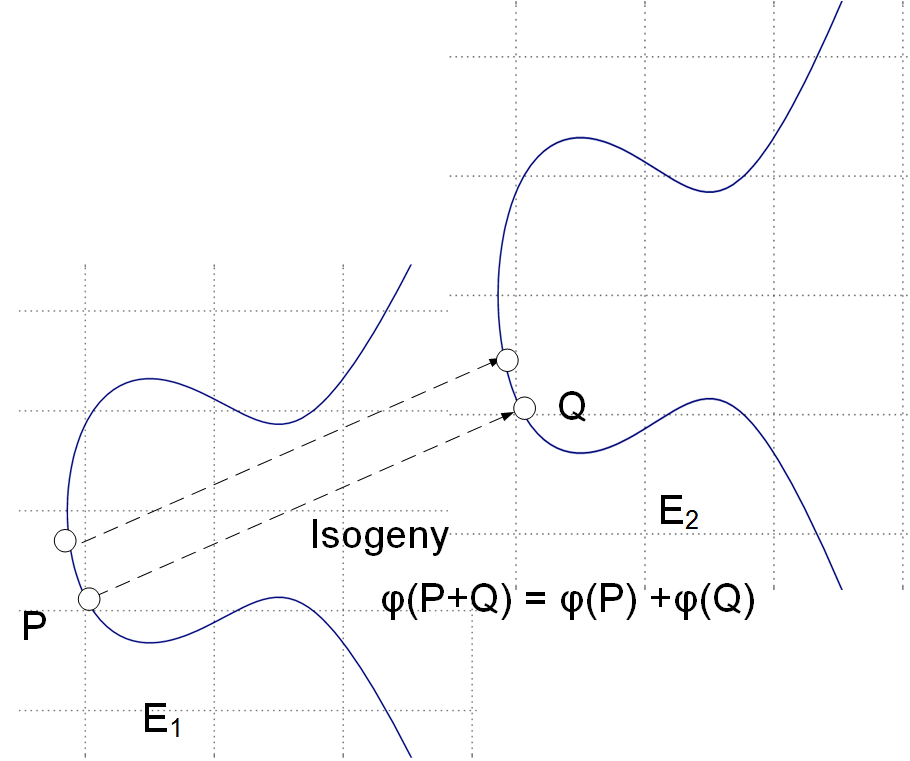
如下图所示,如果我们有两条椭圆曲线(E1和E2),我们可以创建一个函数,将E1上的点(P)映射到E2上的点Q。这个函数被称为同源。如果我们能映射这个函数,E1上的每一点都可以映射到E2。秘密密钥是同源的,公开密钥是椭圆曲线。对于密钥交换,Alice和Bob互相将其同源曲线混合,以生成一条秘密曲线。
因此,SIDH的安全性与寻找两条具有相同点数的超奇异椭圆曲线之间的同源映射问题密切相关。
下面以SKIE为例来说明密钥交换,首先,Alice和Bob从同一条曲线(E0)开始,然后他们随机离开曲线。这就产生了EA (Alice曲线)和EB (Bob曲线)。Alice和Bob相互把他们的曲线发给对方。
然后,Alice再次从EB开始随机行走,并重复她的随机行走。Bob从EA开始行走,重复他的随机行走,然后最终在一条新的秘密曲线处相遇。这是一条只有他们知道的曲线,他们可以用它来创建一个新的密钥,因为没有人知道这条曲线,除非他们知道Bob和Alice的随机行走。
根据Jao-De Feo等人的研究[2],对SIDH的最好攻击是解决相关的claw查找问题,对于经典计算机的复杂度为O(p1/4),对于量子计算机的复杂度为O(p1/6),这表明具有768位质数(p)的SIDH将具有128位的安全级别。
注:claw查找问题是复杂性理论中的一个经典问题。简而言之,给定两个函数f和g,被视为oracle,问题是找到x和y,例如f(x)=g(y)。这对(x, y)被称为claw。
02 性能对比
根据研究人员测试[3],基于同源的方法的性能不如格方法。在该测试中,与目前唯一成为NIST标准密钥封装算法的Kyber相比,SIDH密钥生成、封装和解封装的速度要慢100倍以上。但同时SIDH的密钥长度要小得多。
性能对比:
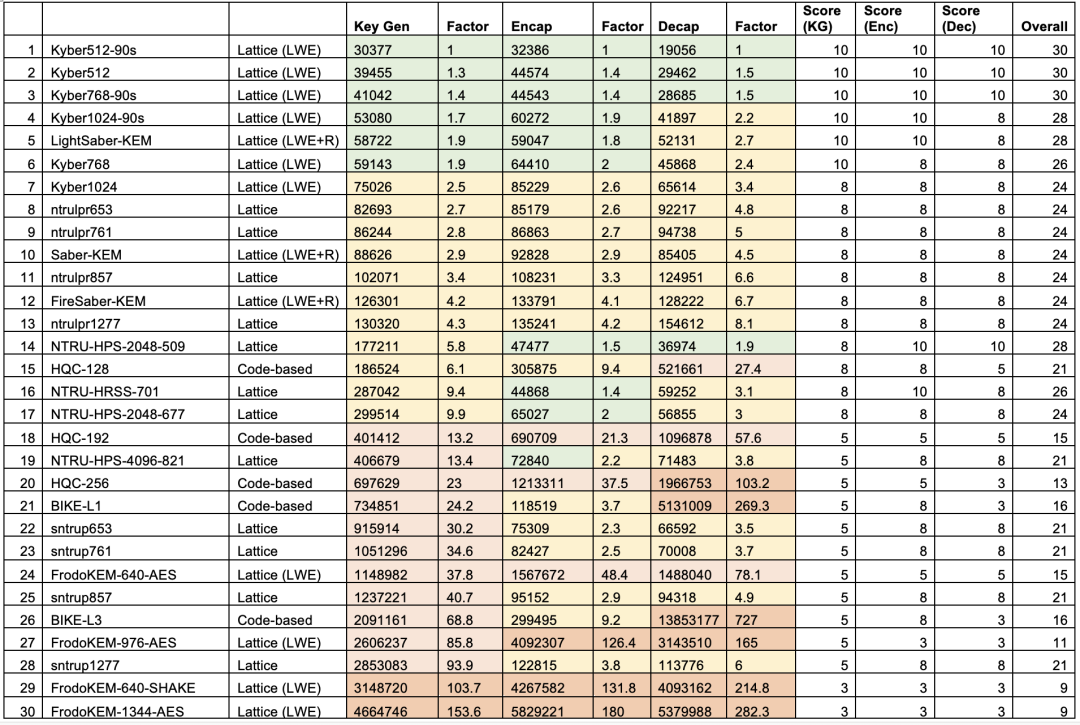
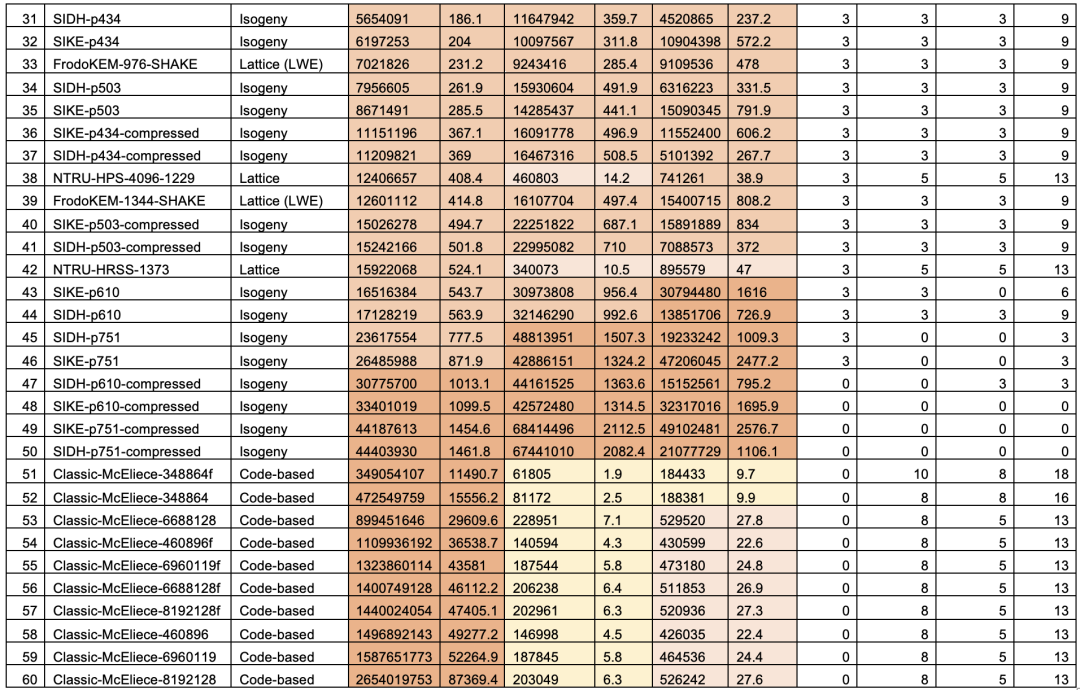
密钥大小对比:
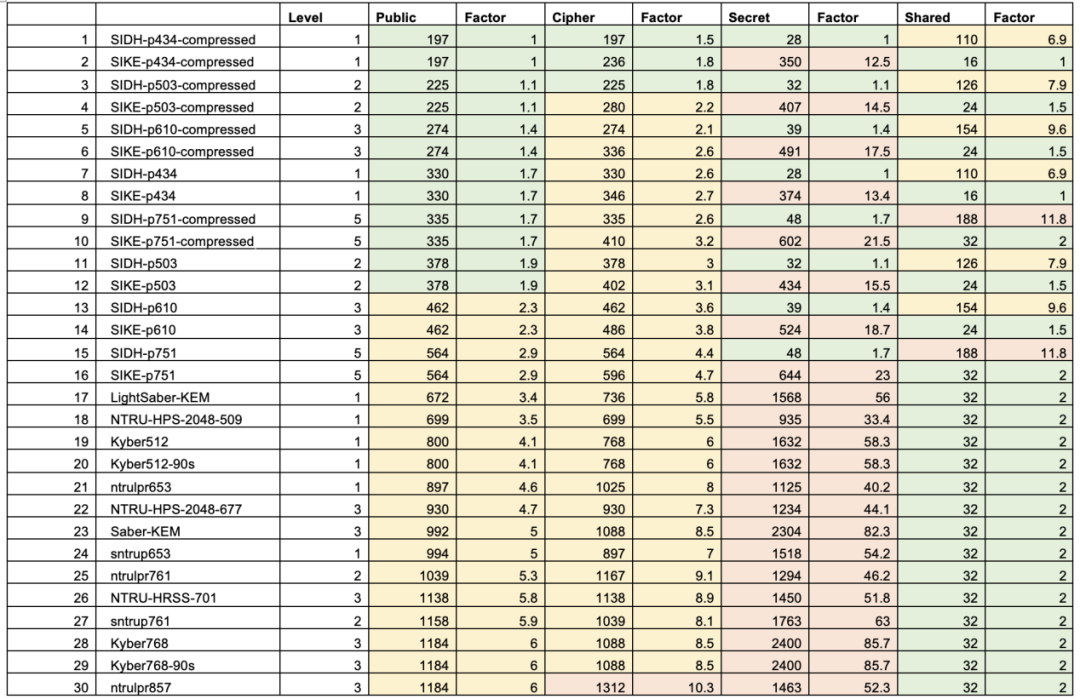

综合来看,Kyber是表现最好的,这也不难理解NIST为什么将其作为标准算法。
参考文献:
[1]https://eprint.iacr.org/2022/975
[2]https://link.springer.com/chapter/10.1007/978-3-642-25405-5_2
[3]https://asecuritysite.com/pqc/pqc_kem
声明:本文来自光子盒,版权归作者所有。文章内容仅代表作者独立观点,不代表安全内参立场,转载目的在于传递更多信息。如有侵权,请联系 anquanneican@163.com。
