全同态加密(fully homomorphic encryption, FHE)方案是一个允许在密文上进行任意复杂运算的密码学系统。一方面,FHE“数据可用不可见”的特性使得云计算场景中诸如云隐私训练的应用成为可能,用户可以在不泄露任何数据的前提下使用算力强但不可信的服务器完成任意计算并获得结果。另一方面,FHE相关概念于1978年被Rivest等人[1]提出,2009年才由Gentry构造出第一个理论证明完全可行的FHE方案[2],历经近30年才获得突破性进展。由此可见无论是功能性还是难度上,FHE当之无愧是现代密码学的圣杯。
到目前为止,所有FHE方案均按照Gentry提出的蓝图实现:(1)先构造一个“有限”FHE方案,所谓“有限”是指在密文能够被正确解密的前提下,方案所能支持的最大运算层数。(2)再通过自举(bootsrapping)将有限FHE方案转化为可以执行任意次计算的FHE方案。Gentry首先基于理想格上的难题设计有限FHE方案,但由于解密算法计算复杂度太高,只能通过引入新的安全假设将解密算法“压缩”(squashing)至可以被有限FHE方案同态运算的级别,再使用自举技术完成FHE方案的构造。后续出现的变种方案DGHV[3]、SV[4]等所基于的安全假设均没有脱离“理想格”(如DGHV方案,仅仅是将代数结构换作整数环),导致实现真正的FHE不可避免地需要引入额外安全假设。这些初代FHE方案不仅理解上困难,所涉及的复杂代数结构和大规模运算也难以在现代计算机器上实现并投入实际生产应用。
初代FHE方案出现不久后,Brakerski等人[5]首次基于容错学习问题(learning with errors,LWE)构建FHE方案,将安全假设从理想格转化到“任意格”上的问题,该方案被称作BV方案。其中BV方案提出的再线性化(relinearization)和维度-模量约减技术成为第二代FHE方案的核心,例如BGV方案[6]中的私钥切换(key switching)和模量切换(modulus switching)实质上是上述两种技术的提炼。再线性化是私钥切换的目的,精确地说,为了防止同态乘后密文长度平方级别增长,通过将原私钥每一位在新私钥下的加密作为辅助信息(通常放入公钥,作为其中一部分),可以将乘法结果密文再线性化为新私钥下的密文。模量切换技术则将噪声增长速度维持在可控状态,防止噪声急剧增长。这些强有力的手段使得诸如BGV[6]、BFV[7]和CKKS[8]等第二代FHE方案可以在不添加额外安全假设的前提下利用自举过程实现真正的FHE。
然而,“再线性化”技术本身带来的大量计算和公钥膨胀问题使得基于现代CPU的软件层面实现难以达到工业界可以接受的性能要求。因此,在现有FHE方案的基础上实现可实际应用的FHE系统,使用并行能力更强的GPU或定制专用硬件加速FHE方案的手段呼之欲出。
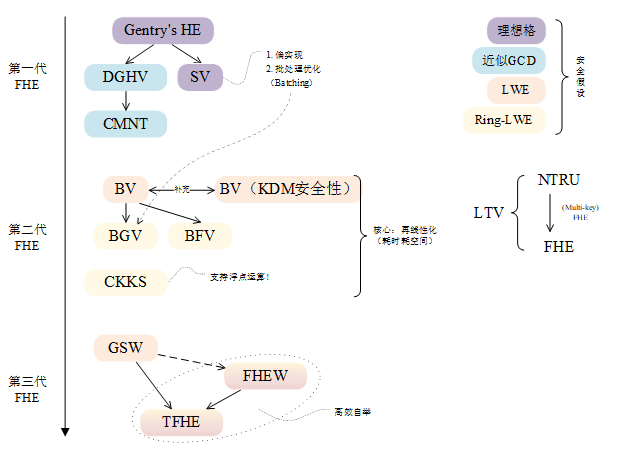
图1 FHE方案发展路线
再来看有关“实现FHE方案”的研究路线。SV方案是第一个支持单指令多数据(Single-Instruction-Multiple-Data,SIMD)操作的FHE方案,也是BGV方案中批处理(batching)优化思想的来源。随后,Gentry等人在实现BGV方案中结合SIMD操作开展了一系列工作,例如文献[9]中使用支持SIMD的快速傅里叶变换(fast Fourier transform,FFT)加速自举过程、文献[10]中展示如何利用SIMD将正在使用的有限域切换为更小的有限域。另一方面,GPU高并行的体系结构使得它在执行并行算法上有着远超现代通用CPU的效率。自NVIDIA公司开发统一计算架构(Compute Unified Device Architecture,CUDA)后,通用计算目的的GPU应用场景逐渐增多,在科学计算、信号处理等不同领域都获得不错的性能提升。基于以上工作和事实,能够看到使用GPU加速FHE方案的可行性和巨大的研究前景,实际上到目前为止,已经有不少相关优秀的研究出现,它们分别针对不同方案和应用层级研究基于GPU的加速算法。
GPU平台上加速各种FHE方案的研究工作已获得不同程度的进展。Wang等人在文章中的工作是GPU加速初代FHE方案(Gentry提出的FHE方案)的首次尝试[11],也是GPU加速FHE方案的最早期工作。他们实际上是将Gentry等人在CPU上的实现[12]适配在GPU平台上,高效执行中间过程中大量可并行处理的向量运算,相比CPU实现的加解密和自举过程获得近7倍的加速比。
Wang等人工作初露锋芒之时第二代FHE方案也随之问世,到目前为止,已经涌现出大量针对诸如BGV、BFV和CKKS等第二代FHE方案的GPU加速方法研究工作。Wang等人的另一项工作[13]是GPU加速BGV方案的早期工作,虽然BGV方案原文中基于LWE和Ring-LWE问题一般化地构造了有限FHE方案,但同时提到基于LWE的BGV方案性能相比基于Ring-LWE的更差,因此实际实现几乎都是基于后者。Wang等人在文章[13]中提到高次数、大系数的多项式模乘运算是BGV方案中最为频繁也最为耗时的基础运算,于是仿照以往工作,设计了由FFT、CRT和Barrett模减等底层基础算子组成的如图2所示多项式环运算系统。
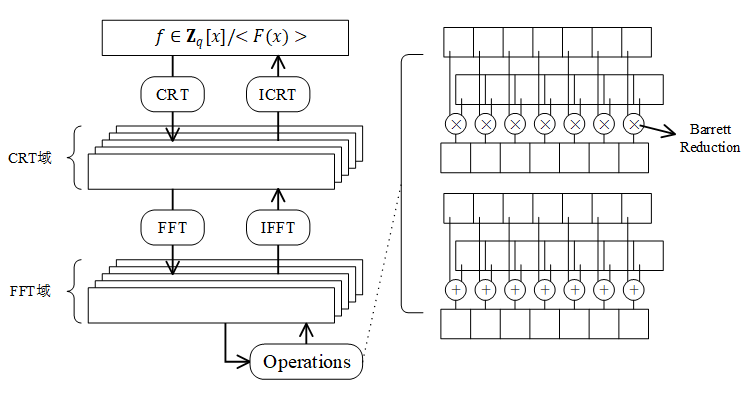
图2 多项式运算系统
从图2可以看出,多项式环运算系统通过中国剩余定理(Chinese remainder theorem,CRT)将多项式分解为多个小模量下的多项式(这样的数据表示方式也被叫作余数系统,residue number system,RNS),再经FFT转化到FFT域中,至此所有多项式运算均转化为向量上的逐项运算,同时每个分量大小不超过机器字长便于使用Barrett约减算法对模乘操作进一步优化。这样的设计能够较大程度地发挥GPU的高并行计算能力,也成为后续所有基于多项式环的FHE方案底层运算库的设计框架。Dai等人[14]将这一框架中复数域的FFT换成有限域上的数论变换(number theoretic transform,NTT),用于加速基于NTRU的FHE方案(也被叫做LTV方案,是第一个满足FHE性质的NTRU加密方案,内部的FHE“工具”基本和BV方案一致,因此同样归为第二代FHE方案)。相比以往,Dai等人的优化工作更注重GPU架构,致力于提升内部流多处理器(stream multiprocessor,SM)的资源利用率以及通过精心设计数据传输路线尽可能减少不必要的访存时延。同时他们的优化工作更为完整,例如Wang等人对BGV的加速工作并未涉及二代FHE方案中特有的“再线性化”过程,仅仅是对底层算子的加速,而文章[14]中则具体分析实际场景中实现再线性化该如何选择底层算子参数,并提出了一些延迟数据移动和利用密文特殊形式跳过冗余操作的技巧,使得整个FHE方案性能获得进一步提升。随后Dai等人从上述工作提炼出二代FHE方案适用的底层多项式运算库cuHE[15],并使用cuHE库结合当时较新的CUDA流技术实现了LTV方案,在单GPU和多GPU上测试AES算法分别获得25倍和31倍的加速比(相比以往GPU上的最优工作)。
再来看第二代FHE方案中另一重要方案BFV,BFV方案原文以“切实可行”为主要目标,基于该方案的GPU加速自然是层出不穷。由于BFV依然是基于Ring-LWE的FHE方案(底层代数结构为多项式环),所以底层运算库基本按照图2实现,近两年中依然有针对该框架的每个模块细致优化的工作出现,如2020年Sahu等人[16]使用GPU加速基于FHE的代理重加密(Proxy Re-encryption,PRE)工作中,BFV版PRE的底层运算库使用NTT算子;同年Kim等人[17]对比分析复数域FFT和有限域NTT的优劣,敏锐地发觉高内存带宽需求是NTT模块的性能瓶颈并提出即时旋转因子优化方案缓解;类似地,2021年Goey等人[18]使用线程束洗牌指令(warp shuffle instruction)等较新GPU技术对NTT模块旋转因子的存储进行优化,区别于以往始终从GPU常量内存或纹理内存读取旋转因子的工作,实现线程束内寄存器交互旋转因子进一步降低访存时延;2022年Özerk等人[19]对NTT模块进行线程级别的优化,实现了单一核函数和多核函数的NTT算法,并在高层级启发式地调用两种实现以大幅提升性能。
除此之外,近年Badawi等人为了实现保持隐私的深度学习预测开展了一系列有关GPU加速FHE方案的研究工作。首先他们同样按照图2设计框架实现支持BFV方案的底层多项式运算库,不同的是,他们将FFT模块具体实现为离散伽罗华变换(discrete Galois transform,DGT)[20],这也是DGT第一次被引入GPU加速FHE方案的研究中。DGT技术可以看做是NTT加速多项式乘法的进一步优化,DGT对应数域为伽罗华域GF(p2),该数域与复数域中实部虚部均为整数的子域同构,自然可以与NTT数域上的一对整数建立双射,因此使用DGT可以让变换长度减半,所需存储的旋转因子减半。使用DGT加速BFV方案所需多项式乘法的相近工作还有Alevs等人[21]的研究,区别在于他们更注重软件层层面适配GPU架构的优化工作,例如他们提出一种分层DGT技术可将大DGT块化为多个小DGT块,再通过细粒度的FFT算法计算这些小DGT块(如图3所示,其中N=√N×√N是文中推荐的分层方式),尽可能减小DGT计算过程中的数据依赖以便按照访存合并的方式编排线程读取数据,最终降低访存时延。

图3 分层DGT
随后,Badawi等人进一步在GPU上实现了BFV方案的两种优化版本BEHZ和HPS,并在GPU上对比测试分析两种优化方案性能上的优劣[22]。实验结果表明,随着同态运算电路乘法深度的增加,HPS优化方案的性能始终优于BEHZ优化方案,最终在128位安全性、最大乘法深度设为98(该深度支持很多应用,例如深度学习网络、逻辑回归等机器学习算法)的条件下,将解密和同态乘的执行时间分别降至0.5ms和51ms,离实际应用更近一步。紧接着,Badawi等人更进一步将单机加速BFV方案工作扩展至多GPU上[23],他们将RNS下的多项式数据按合理行列分块的方式分布于多个GPU,保证每台机器计算负载平衡,同时设计了GPU对GPU的通信协议以提升GPU之间的数据交换效率。最后,Badawi等人将上述GPU加速BFV方案的工作具体应用于深度学习领域,实现了第一个GPU加速的同态卷积神经网络(Homomorphic convolutional neural networks,HCNN)并使用训练好的模型在加密图像上进行预测[24],完成了FHE的实际应用。
为了实现诸如隐私数据分析和训练这些更广泛的应用,上面提到的各种加速工作所实现的FHE方案均无法满足要求,而CKKS方案支持浮点数运算的特性成为目前解决FHE实运算最有前景的FHE方案,同样出现了许多研究工作。Jung等人[25]对CKKS方案作者开源的代码库进行实际测试分析,提出不同参数下分析HE关键操作计算复杂度和数据传输模式的方法,并基于此给出CPU和GPU平台上加速CKKS方案的优化方案。很快Jung等人在另一个工作[26]中实践了上述分析方法,同时提出“摊销同态乘法时间”概念并将其作为比较性能差异的一个新指标,最终实现GPU平台上第一个支持自举的CKKS方案。
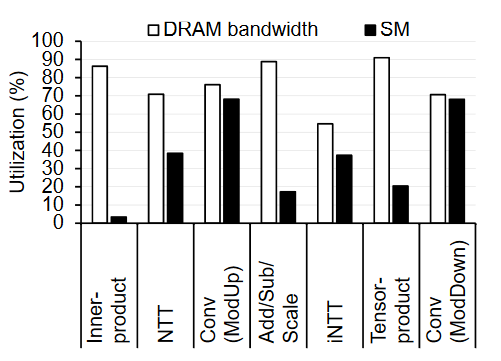
图4 GPU资源利用率[26]
他们通过上述分析及实际测试发现(如图4),执行CKKS方案内部基础算子时,绝大多数情况都是DRAM带宽利用率高于SM利用率,因此在算法完全适配GPU架构的前提下,高带宽需求才是GPU加速FHE方案的性能瓶颈。为了解决上述问题Jung等人提出以内存为中心的优化方案,可以归纳为核函数融合技术,即将基础算子合并或更大粒度地将部分FHE操作合并,减小DRAM的访问次数,最终获得超过100倍加速比(相比单线程CPU获得257倍加速比)的性能提升。
除针对特定FHE方案的加速工作,也有探索多个FHE方案模式参数化设计工作。Liu等人[27]设计的CARM系统涵盖BGV、BFV和CKKS这些基于Ring-LWE的二代FHE方案,底层运算库依然按照图2实现,但同时针对物联网系统面向多平台的应用场景,分别实现性能优先和内存节省优先两种版本的底层算子达到根据目标平台灵活选择最优方案的目的。由于是GPU加速FHE方案的最新研究,Liu等人也提出类似文章[26]中以内存为中心的核函数融合和数据复用技术,获得线程级别和指令级别并行上的平衡。
当然还有大量结合FHE的实际应用,这些工作一般都根据特定场景选择合适的FHE方案,并且直接将上面很多GPU加速FHE方案作为底层接口使用,在高层级设计FHE的具体应用。另外,本文缺少对第三代FHE方案的描述,事实上诸如GSW、FHEW和TFHE方案结合GPU加速的相关工作目前比较稀缺,但是它们自举过程高效的特性不容小觑,故GPU加速FHE研究仍有很长路要走!(陈祎、华强胜)
参考文献:
Rivest R L, Adleman L, Dertouzos M L. On data banks and privacy homomorphisms[J]. Foundations of secure computation, 1978, 4(11): 169-180.
Gentry C. Fully homomorphic encryption using ideal lattices[C]//Proceedings of the forty-first annual ACM symposium on Theory of computing. 2009: 169-178.
Dijk M, Gentry C, Halevi S, et al. Fully homomorphic encryption over the integers[C]//Annual international conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 2010: 24-43.
Smart N P, Vercauteren F. Fully homomorphic encryption with relatively small key and ciphertext sizes[C]//International Workshop on Public Key Cryptography. Springer, Berlin, Heidelberg, 2010: 420-443.
Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE[J]. SIAM Journal on computing, 2014, 43(2): 831-871.
Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory (TOCT), 2014, 6(3): 1-36.
Fan J, Vercauteren F. Somewhat practical fully homomorphic encryption[J]. Cryptology ePrint Archive, 2012.
Cheon J H, Kim A, Kim M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]//International conference on the theory and application of cryptology and information security. Springer, Cham, 2017: 409-437.
Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Springer, Berlin, Heidelberg, 2012: 1-16.
Gentry C, Halevi S, Peikert C, et al. Ring switching in BGV-style homomorphic encryption[C]//International Conference on Security and Cryptography for Networks. Springer, Berlin, Heidelberg, 2012: 19-37.
Wang W, Hu Y, Chen L, et al. Accelerating fully homomorphic encryption using GPU[C]//2012 IEEE conference on high performance extreme computing. IEEE, 2012: 1-5.
Gentry C, Halevi S. Implementing gentry’s fully-homomorphic encryption scheme[C]//Annual international conference on the theory and applications of cryptographic techniques. Springer, Berlin, Heidelberg, 2011: 129-148.
Wang W, Chen Z, Huang X. Accelerating leveled fully homomorphic encryption using GPU[C]//2014 IEEE International Symposium on Circuits and Systems (ISCAS). IEEE, 2014: 2800-2803.
Dai W, Doröz Y, Sunar B. Accelerating NTRU based homomorphic encryption using GPUs[C]//2014 IEEE High Performance Extreme Computing Conference (HPEC). IEEE, 2014: 1-6.
Dai W, Sunar B. cuHE: A homomorphic encryption accelerator library[C]//International Conference on Cryptography and Information Security in the Balkans. Springer, Cham, 2015: 169-186.
Sahu G, Rohloff K. Accelerating lattice based proxy re-encryption schemes on gpus[C]//International Conference on Cryptology and Network Security. Springer, Cham, 2020: 613-632.
Kim S, Jung W, Park J, et al. Accelerating number theoretic transformations for bootstrappable homomorphic encryption on gpus[C]//2020 IEEE International Symposium on Workload Characterization (IISWC). IEEE, 2020: 264-275.
Goey J Z, Lee W K, Goi B M, et al. Accelerating number theoretic transform in GPU platform for fully homomorphic encryption[J]. The Journal of Supercomputing, 2021, 77(2): 1455-1474.
Özerk Ö, Elgezen C, Mert A C, et al. Efficient number theoretic transform implementation on GPU for homomorphic encryption[J]. The Journal of Supercomputing, 2022, 78(2): 2840-2872.
Al Badawi A, Veeravalli B, Mun C F, et al. High-performance FV somewhat homomorphic encryption on GPUs: An implementation using CUDA[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2018: 70-95.
Alves P G M R, Ortiz J N, Aranha D F. Faster homomorphic encryption over GPGPUs via hierarchical DGT[C]//International Conference on Financial Cryptography and Data Security. Springer, Berlin, Heidelberg, 2021: 520-540.
Al Badawi A, Polyakov Y, Aung K M M, et al. Implementation and performance evaluation of RNS variants of the BFV homomorphic encryption scheme[J]. IEEE Transactions on Emerging Topics in Computing, 2019, 9(2): 941-956.
Al Badawi A, Veeravalli B, Lin J, et al. Multi-GPU design and performance evaluation of homomorphic encryption on GPU clusters[J]. IEEE Transactions on Parallel and Distributed Systems, 2020, 32(2): 379-391.
Al Badawi A, Jin C, Lin J, et al. Towards the alexnet moment for homomorphic encryption: Hcnn, the first homomorphic cnn on encrypted data with gpus[J]. IEEE Transactions on Emerging Topics in Computing, 2020, 9(3): 1330-1343.
Jung W, Lee E, Kim S, et al. Accelerating fully homomorphic encryption through architecture-centric analysis and optimization[J]. IEEE Access, 2021, 9: 98772-98789.
Jung W, Kim S, Ahn J H, et al. Over 100x faster bootstrapping in fully homomorphic encryption through memory-centric optimization with GPUs[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021: 114-148.
Shen S, Yang H, Liu Y, et al. CUDA-Accelerated RNS Multiplication in Word-Wise Homomorphic Encryption Schemes[J]. Cryptology ePrint Archive, 2022.
声明:本文来自穿过丛林,版权归作者所有。文章内容仅代表作者独立观点,不代表安全内参立场,转载目的在于传递更多信息。如有侵权,请联系 anquanneican@163.com。
