1引言

新世纪以来，我国互联网行业快速发展与技术、业务创新的同时，伴随而来的是各类安全性问题。安全问题并非新事物，而是自计算机软件开始大规模工业化应用起，就一直与计算机应用、业务一起共同变化。与软件时代相比，安全问题也从设计需求到实现落地上，产生了极大的变化。主要体现在安全战线被迅速拉长与新技术、新架构形式、爆发式的对中低层次研发人员的需求增长，给安全架构与安全性设计带来全新的巨大挑战：安全对抗从传统的网络、协议、系统、应用与桌面层次，迅速转化为快速变化、快速迭代中的业务流程、业务逻辑、逻辑与流程实现方面的全方位对抗。新技术、新架构形式爆发式的增长与整个互联网业务形态决定了，支撑其业务的技术、架构设计，考虑的就是要满足大流量、高并发、低成本、错误快速恢复、高冗余等指标。如何设计才能在不降低框架、架构、设计、流程的使用、运行成本的基础上，有效的提升编码的安全性，至今都仍是安全从业者们关注的重点。

2012年之前，行业内的看法大多趋向于从事前培训与发现、事中监控与阻断、事后审计与总结三个方面建设、构建企业安全体系。而后TSRC（腾讯安全应急响应中心）的成立，引入了白帽子协助企业发现安全问题。这一全新的理念，迅速为广大安全工作者接受。SRC模式改变过去企业安全与白帽子、自由安全研究员在安全技术上合作但是在安全业务上对抗的模式，主动与白帽子、自由安全研究员合作，对提供有效漏洞、安全情报、安全缺陷的报告提交者以一定的奖励。如此则既避免了白帽子与自由安全研究员在研究、探索安全技术时潜在的法律安全风险点，又给企业提供了一个以低成本，按效果付费的外源性安全问题发现机制。

安全漏洞、安全情报、安全设计缺陷，一般按照问题的影响，分为：严重、高危、中危、低危、BUG/无影响、非漏洞几个等级。所以SRC之于企业，最大的价值在于挖掘企业安全建设过程中自身难以覆盖的业务层面的高危、严重等级的安全性问题。如何界定SRC的价值，以及如何更好的通过运营活动持续提升SRC对于企业的价值是近几年来企业安全工作者们讨论的重点。通常认为漏洞报告数量是用于与企业安全建设中，发现的内源性安全性漏洞数量进行对比，衡量SRC在总的安全性问题上覆盖率的指标；优质漏洞数量（严重及高危）为衡量SRC对企业安全建设中，不在自身覆盖范围内的安全问题覆盖程度的指标。

本文通过对58业SRC上线以来的漏洞报告提交数、优质漏洞报告提交数与注册白帽子数量、运营活动之间的关系进行分析。为企业SRC运营活动的开展方式、目标，SRC建设方向与核心指标的提取提供有意义的建议。

2数据来源、数据预处理与数据介绍

2.1数据来源

本文实证分析与研究，选取的是58SRC自上线至写作时止，共166天的数据。原始数据包含按日统计的：新增漏洞报告数、新增优质漏洞报告数、新增注册白帽子数、当日开展了哪些运营活动。

2.2数据预处理

在数据预处理阶段，对原始数据进行了变换。首先是对当天没有新增漏洞报告、新增优质漏洞报告、新增注册白帽子的各行做补0处理，整体对齐166天范围的时间序列数据。然后将日期转化为与日期无关从1开始的纯数字序列。最后是新增了一列截止当日注册白帽子总数的变量。

2.3数据介绍

为叙述方便，后续以英文命名变量，各变量含义见下表：

虚拟变量的设置

上表变量中，openDouble、springDouble、icqDouble、juneDouble为虚拟变量。当变量对应的运营活动正在进行时取值1，否则取0。四次运营活动里，任意两个均未同时进行过，不需要考虑虚拟变量陷阱问题。如下图所示。

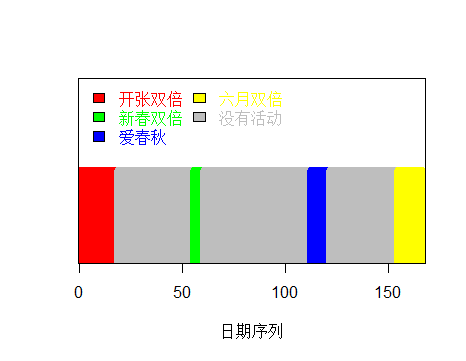
图1 运营活动开展时间示意

SRC上线、六月两次活动的形式为：对所有的漏洞报告均给予双倍奖励；春节、爱春秋两次活动的形式为：仅对漏洞报告评级为高危及严重的给予双倍奖励。从活动形式上SRC上线、六月与春节、爱春秋对整体SRC运营影响的方式是不一样的，故这两类形式不同的活动虚拟变量应该分开，不能共用一个变量。

由于有较多外部白帽子、自由安全研究员在SRC上线前就已经掌握了大量漏洞信息；而上线六个月后，大部分积压漏洞报告已经报告完毕。故SRC上线与六月两次活动对整体SRC运营的影响程度也不一样，这两个运营活动需要单独设置虚拟变量。春节期间大多数白帽子、自由安全研究员挖掘安全漏洞的积极性有所下降；爱春秋活动是由若干厂商赞助的安全技术沙龙。故春节和爱春秋两次活动对整体SRC运营的影响范围与影响程度也不一样，对这两个运营活动也需要单独设置虚拟变量。

数据整体变化趋势

前表设置的非虚拟变量，整体呈现SRC上线时数值或增量特别大，之后逐渐趋于平缓；但在部分运营活动开展时，局部数值或增量略有变化的趋势。数据的整体走势如下两图所示：

图2 新增注册白帽子与总注册白帽子数量随时间变化趋势

图3 每日新增漏洞报告与高危以上漏洞报告数量随时间变化趋势

从图中可以看出，newVulAll与newVulHigh的变化有时趋势一致，有时与newUser的变化一致。初步考虑三者存在相关性。(其实上面的图看不清楚，因为一开始的数值太大了。取对数后重新画一次，看下面两个图)

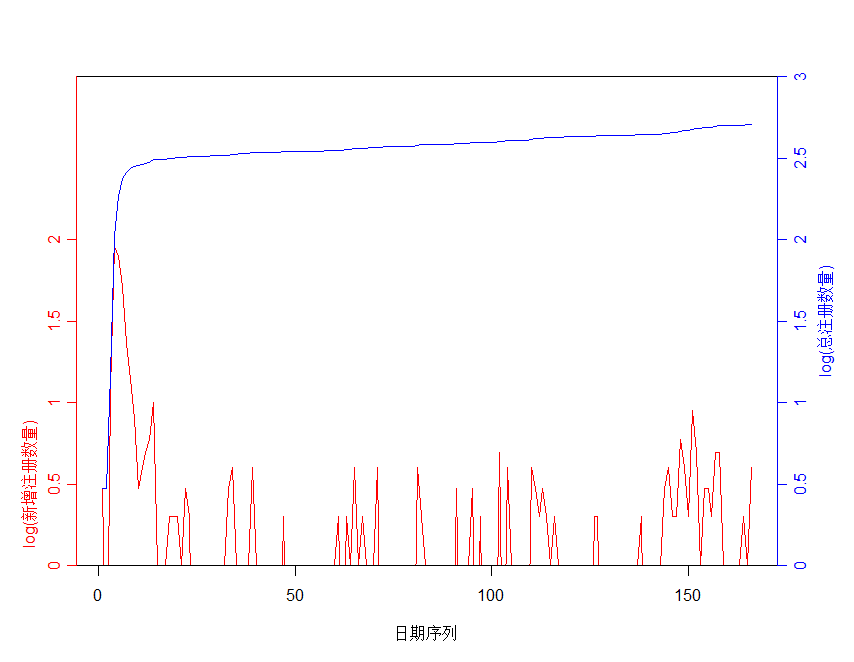
图2改 新增注册白帽子与总注册白帽子数量随时间变化趋势

图3改 每日新增漏洞报告与高危以上漏洞报告数量随时间变化趋势

2.4数据的平稳性检测

在对时间序列开始分析前，先对数据做平稳性检验。ADF平稳性检验原理来自：对于时间序列D，通常能找到一组常数α、β、γ，使得时间序列D能满足以下四组方程中的某一组：

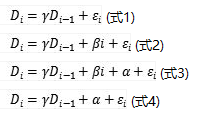
其中ɛ_i为随机扰动,对∀i有 ɛ_i~N(0, σ²)；且对∀ t、j，若t≠j，则有COV(ɛ_t,ɛ_j)=0。对于上述三式，若|γ|=1时，称时间序列D存在单位根，整个时间序列D有可能会退化为一个随机游走序列，不满足平稳性要求，可能产生伪回归问题；若|γ|<1时，从长期来看，前序序列对后序序列的影响逐渐归0，满足平稳性要求，可以进行回归分析；若|γ|>1时，从长期来看，前序序列对后续序列的影响被不断放大，亦不满足平稳性要求，极可能产生伪回归问题。若序列不满足平稳性要求，则当且仅当自变量与因变量满足协整条件时，回归分析产生的对数据的拟合模型才是有意义的。

userTotal实际是来自newUser变量的历史值求和，应该存在非平稳问题。但是若对userTotal变量求差分，产生的实际结果则是newUser变量。如此则会影响回归模型对实际问题的解读。出于严谨性考虑，现对newVulAll，newVulHigh，newUser，userTotal四个变量均进行了平稳性检测。检测结果如下表：

表1：各变量平稳性检测结果

(实际上，除了userTotal变量不能在式1下通过检验，其他所有拟合式、所有变量都能检验通过，具体看r代码吧，有注释。式2实际上是式3取α=0时的特例。看了下ur.df包，trend模式时允许α=0，就不单独再尝试式2了)

结论：newVulAll，newVulHigh，newUser，userTotal四个变量均在1%的显著性水平下通过了平稳性检验。

3模型回归、结果分析和初步结论

3.1模型回归原理

多元线性回归假设因变量与自变量之间，无论在实际总体还是样本观察值里，都存在如下两式所示的线性近似关系：

令因变量为y，具体样本值表示为y_t；自变量为x_i，具体的样本值表示为x_it，那么有，

其中ɛ和ɛ_t为服从均值为0正态分布的随机扰动项，且满足以下假设：

对ɛ和ɛ_t，有

可以证明，从合理抽样的样本中计算出的式6中的各常数和系数，是对于总体式5中各常数和系数的无偏估计量。

具体计算常数项与各自变量系数的常用方法为最小二乘法，即：忽略随机扰动项；直接将样本值带入式2，得到自变量为γ_i和β的回归曲线；构造所有样本点距离特定γ_i和β的回归曲线时的残差平方和函数；由于x_i之间独立不相关，故γ_i之间也独立不相关，可以分别对γ_i和β求偏导，以寻找各自的极值；寻找、计算合适的γ_i0和β₀组合以使得残差平方和函数值最小。此时找到的γ_i0和β₀组合即为对式6中γ_i和β的最大似然估计值（公式略）。

由于回归模型成立的条件预设有上述式8的条件，而实际应用过程中，时间序列有可能会不满足式8所述的条件，这种情况称为异方差。当异方差出现时，如果仍然按照同方差的假设进行回归，则会出现检验结果偏向乐观，对本不应该通过检验的回归方程或系数更乐观的被判定为通过检验。故每个模型回归完成时，还需要检查是否存在异方差。

通常采用white检验来进行异方差检测。用于模型回归的样本出现异方差时，若使用普通的标准差，则会导致模型评估不准确。此时需要改用robust稳健标准差再次对回归模型进行评估。

3.2对每日新增漏洞报告总数建立回归模型

直接以newVulAll作为因变量，以newUser,userTotal,openDouble,springDouble,icqDouble,juneDouble作为自变量尝试建立回归模型，结果如下表： 

表2：对newVualAll变量直接回归的结果

怎么看上面这个表？科普君上线：

1. 常数项的t检验结果无意义，通常不看；标准差仅表示样本集中该变量的样本标准差，通常也不看。即：上表中灰色部分通常不关注。

2. 各变量回归系数采用双边t检验，有兴趣自己查t统计量表，没兴趣直接看p值

3. R2和调整R2值介于0-1之间，值约大，说明模型对样本数据的拟合程度越高

4. f统计量有兴趣自己查f统计量表，没兴趣直接看p值

5. p值介于0-1之间，值约小，说明“本变量的系数”或“回归模型”越可信；为什么概率越小越可信的问题超出本文范围，请自行学习统计学中“假设检验”部分知识

6. 后面本文作者将不会再从图片里面把表格画出来了，作者还要搬砖修bug，请各位看官自行脑补表格

从上表可知，此回归模型的模型调整后的可决系数R²为0.8905，p值为2.2×10^-16，整体拟合度很高；但是其中“爱春秋双倍奖励活动”的回归系数为负数，运营活动通常不可能对整体呈负作用的贡献，且回归系数未通过检验；同时还存在“春节双倍奖励活动”的回归系数未通过检验的问题。对此两个问题，有两方面的考虑：一、运营活动的虚拟变量可能分配和设置不当，相互之间可能存在多重共线性问题，可能产生了伪回归。 二、“爱春秋双倍奖励活动”或“春节双倍奖励活动“对漏洞报告提交数量几乎无影响，导致对应的虚拟变量实际在回归时应该被归纳为无关变量。具体是哪种原因或者两种原因都有，需要进一步从模型参数检测与实际运营数据进行比对给出结论。

首先检验问题一。对于模型中是否存在多重共线性，一般利用方差膨胀因子来评估。可以证明，对变量x_i,其对应的回归估计系数γ_i的方差可以表示为：

其中

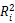
为x_i的可决系数。方差膨胀因子即为上式里的右项，即：

如果VIF>5，说明模型中存在变量间的多重共线性；如果VIF>10，说明模型中存在严重的变量间多重共线性。当出现多重共线性时，可以使用逐步回归法得到更优的回归结果。

检测结果见下表：

表3：newVulAll变量原始回归模型的方差膨胀因子

小结：所有参数系数的方程膨胀因子均小于5，不认为各个变量间存在多重共线性。故变量的设置不存在多重共线性。

现在验证问题二。若icqDouble或springDouble确实为对整体几乎无影响的变量，则去掉其中之一或两者都去掉后，对回归方程的调整R²应该影响不大或调整R²增大，且整体的回归方程也应该继续能通过检验；若只去掉其中一个变量，则回归方程中，另一变量的系数应该依然通不过检验。同理，对其余三个变量依次验证。（后面的另外两次回归，我就不手工去掉变量了，反正结果是和逐步回归的结果是一样的）

去掉icqDouble变量后再次进行回归的结果,如下表：

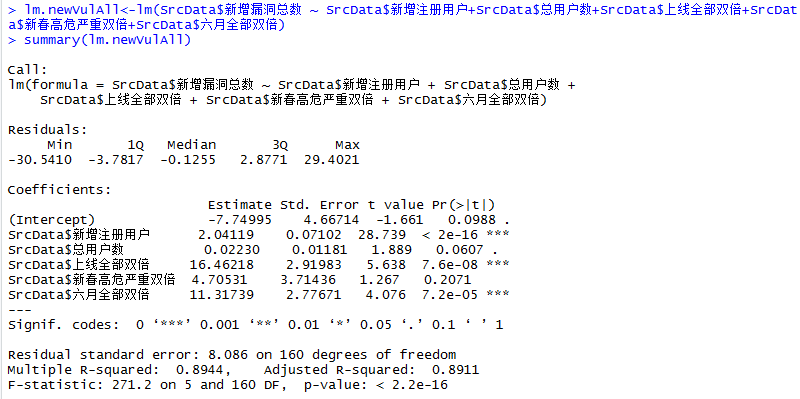
假装有表4：去掉icqDouble变量后的回归情况

小结：springDouble的系数依旧不能通过检验；调整R²增大；模型整体通过检验；icqDouble很可能为与因变量无线性关系的变量。

去掉springDouble参数后再次进行回归的结果：

假装有表5：去掉springDouble变量后的回归情况

小结：icqDouble的系数依旧不能通过检验；调整R²减小；模型整体通过检验；springDouble为与因变量无限性关系的变量。

两个参数都去掉后再次进行回归的结果：

假装有表6：去掉icqDouble和springDouble变量后的回归情况

小结：所有参数在10%的显著水平下通过检验；调整R²增大；模型整体通过检验。再对异方差进行检测。这里采用Breusch-Pagan检测法。在该检测法中，采用如下假设：

H0:回归模型中不存在异方差；H1:回归模型中存在异方差

检测结果:

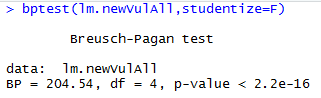
假装有表7：newVulAll的回归模型异常检测结果      

小结：p值<0.1，结果显著，拒绝回归模型中不存在异方差的备则假设。

声明：本文来自58安全应急响应中心，版权归作者所有。文章内容仅代表作者独立观点，不代表安全内参立场，转载目的在于传递更多信息。如有侵权，请联系 anquanneican@163.com。