刚刚,科学家Ed Gerck在领英宣布:“量子计算 (QC) 已成为现实。我们破解了 RSA -2048 密钥。”
下图为发文:
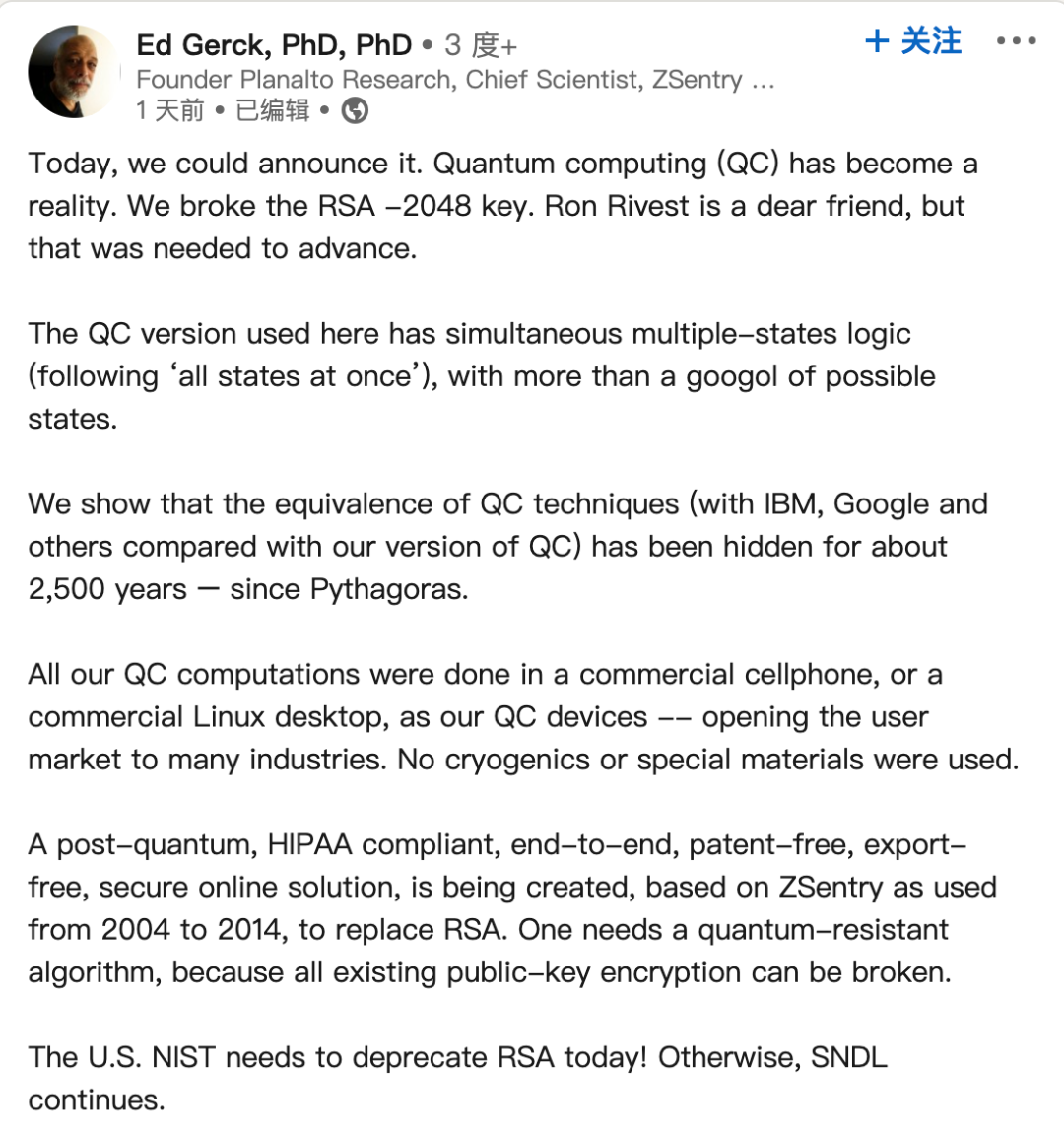
Ed Gerck,何许人也?
根据他在 LinkedIn 上的个人资料显示,Gerck是一名物理学博士,是加利福尼亚州一家名为 Planalto Research 公司的创始人兼首席科学家,ZSentry 架构师。
消息一出,引来了多名密码学家和安全专家的质疑,大致可以概括为:如果属实的话,听起来不错,但你能证明这一点吗?
许多密码学家认为,破解 RSA -2048 的最可行的方法是将涉及使用 Peter Shor 在 1994 年开发的量子算法来查找整数的素因数,一旦构建了足够强大的量子计算机,就可以运行该算法来破解 RSA 等密钥。
英国萨里大学计算机科学教授Alan Woodward表示:“通常会在量子计算机中使用 Shor 算法来尝试破解 RSA,但目前还没有任何量子计算机能够产生足够的门来破解 RSA -2048。如果 RSA-2048 被破解,我会感到非常惊讶”。
然而,如果要建造一台可以破解RSA密码的量子计算机,需要数百万甚至数十亿个物理量子比特。其中只有数万个真正用于计算,也就是所谓的逻辑量子比特(logical qubits);其余的将需要用于纠错,以此用来补偿退相干问题。
值得注意的是, 当前,所推出的最高的量子计算机的比特数量,也才1180个量子比特而已。
Gerck 表示:“他所有的QC 计算都是在商用手机或商用 Linux 桌面上完成的,资本成本不到 1,000 美元。没有使用低温或特殊材料。”
也就是说,原本要耗资可能+∞的资金,而且可能要在多年后量子计算机才能达成的目标。现在,基于1000美元以内即可完成破解RSA密码。
对于全球都在狂追量子计算的国家、公司而言,震不震惊?意不意外?
然而,这一宣称并非空穴来风。
Ed Gerck就此还提交了与科学家Ann Gerck合著的研究论文的预印本[3],标题为“QC Algorithms: Faster Calculation of Prime Numbers”。

根据论文,我们可以获取到几个重要消息:
可以实现对十进制数超过 101000 位的数字进行因式分解
所有的QC计算都是在商用手机或商用 Linux 桌面上完成
没有使用低温或特殊材料
资本成本不到 1,000 美元
使用的量子计算(QC)版本具有同时多状态逻辑(遵循“一次所有状态”),具有多种可能状态
独特的QC技术,与 IBM、Google 和其他公司不同,自毕达哥拉斯以来,已经被隐藏了大约 2,500 年
Woodward在审阅了Gerck的研究论文后表示:“这似乎是所有理论都证明了各种猜想——而这些证据肯定是有问题的,当人们可以向他们发送 RSA 模数进行因子分解并返回两个素数时,我就会相信他们已经做到了这一点。在我看到这一点之前,我只是感到困惑,并且不相信他们已经做到了其所宣称的那样。”
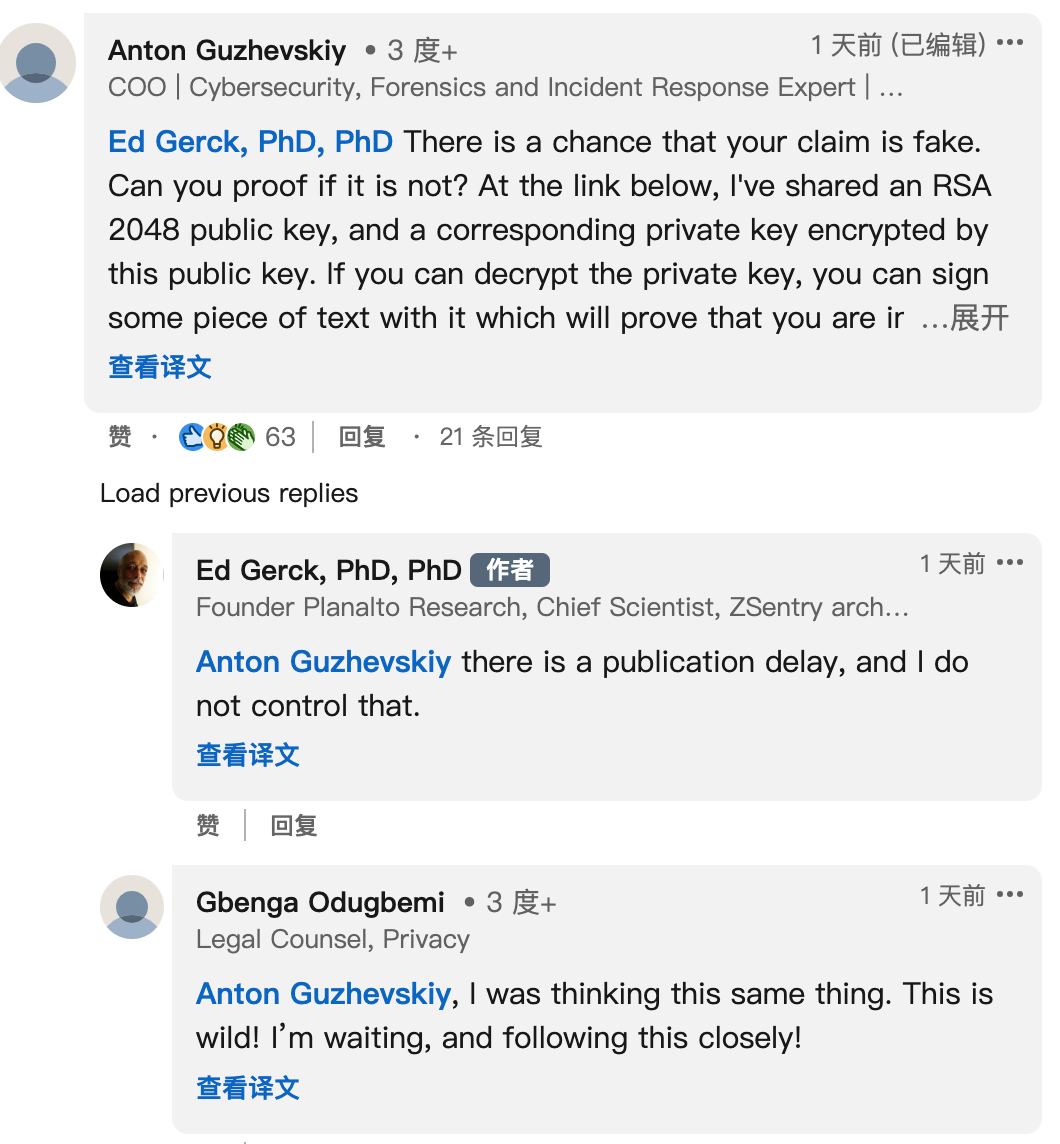
澳大利亚网络安全公司 ThreatDefence 的首席运营官Anton Guzhevskiy也要求Gerck证明他的说法。
Guzhevskiy在 LinkedIn 上回复 Gerck 的帖子时说道:“我共享了一个 RSA-2048 公钥以及由该公钥加密的相应私钥。如果您可以解密私钥,则可以用它签署一些文本,这将证明您拥有该私钥。你可以做到吗?”
Gerck 的回答是:“出版有延迟,我无法控制。”
论文显示,所有现有的公钥加密都可以被破解,Gerck团队正在基于 2004 年至 2014 年使用的 Z Sentry,创建一种后量子、符合 HIPAA 要求、端到端、无专利、无出口、安全的在线解决方案,以取代 RSA。
同时,Gerck还呼吁,美国 NIST 今天需要弃用 RSA!否则,SNDL (现在存储稍后解密)将继续。
这一爆炸性消息到底真实与否,是否如前期常温超导一样,是一场闹剧,还有待同行评审的发表。
如果 Gerck 的说法属实,那么对于任何仍在使用 RSA 加密敏感数据的政府和组织来说,这都是一个非常糟糕的消息,可以想象一下,如果所有的私密、敏感数据都将可能公之于众,会造成什么样的后果?
这,就不仅仅是一个大新闻了。
引用:
[1]https://www.linkedin.com/posts/edgerck_today-we-could-announce-it-quantum-computing-activity-7125215279688601600-XPso?utm_source=share&utm_medium=member_desktop
[2]https://www.govinfosecurity.com/us-government-picks-quantum-resistant-encryption-algorithms-a-19509
[3]https://www.researchgate.net/publication/373516233_QC_Algorithms_Faster_Calculation_of_Prime_Numbers
声明:本文来自量子客,版权归作者所有。文章内容仅代表作者独立观点,不代表安全内参立场,转载目的在于传递更多信息。如有侵权,请联系 anquanneican@163.com。
