
截至撰文时间2024年1月22日17:00,Y2Q倒计时还有六年158天20时
未来的量子计算机将远远超越目前的计算机,有能力破解维护我们通信安全的密码。
全世界的数字安全专家都在关注Y2Q——即“量子年”(Years to Quantum),它在计时,直到量子计算机能够攻破现代密码学。
公钥加密技术因其在公开场合共享密码的巧妙方法而被称为“公钥加密技术”(public-key cryptography),它确保了网上购物时信用卡号码的安全,并验证手机软件更新的真实性,以防止黑客入侵。
举报人用它联系记者,企业用它发送机密文件。
然而,量子计算机将导致标准的公钥加密技术失效。
云安全联盟量子安全工作组联合主席布鲁诺·胡特纳(Bruno Huttner)解释说:“这确实非常严重。如果明天就有一台量子计算机,我们将无法以任何安全方式在一起交谈。”
胡特纳是Y2Q时钟的创造者之一,Y2Q时钟的命名是为了类比20世纪90年代末的千年虫危机。
在20世纪,软件程序只使用两位数表示年份,这导致计算机将2000年解释为00,与1900年相同。
然而,当新千年到来时,企业和政府迅速修复了涉及这一日期的程序,避免了潜在的大规模混乱。
没有人知道量子计算机何时会被开发出来,足以打破密码标准。目前,Y2Q时钟上的结束日期定为2030年4月14日——尽管只是一种猜测。
但大多数研究人员认为,这种变革将在未来几十年内发生。
对于需要长期保密的政府和其他机构来说,真正的最后期限要早得多。
如果今天发送的加密数据被存储起来,未来的量子计算机就可以追溯性地解密这些信息。
密歇根大学的计算机科学家克里斯·佩克特(Chris Peikert)说:“如果你需要在20年内保守秘密,而20年内可能会出现破解加密技术的量子计算机,那么你现在可能已经遇见问题了。”
为了应对这一威胁,美国国家标准与技术研究院(NIST)于2016年启动了一场公开竞赛。
该竞赛征集“抗量子”密码:这些密码可以在当今的计算机上运行,但却非常强大,甚至量子计算机也无法破解。
2022年12月,美国国会通过了《量子计算机网络安全准备法案》,要求政府机构制定向此类算法过渡的计划,凸显了该法案的紧迫性。
经过四轮提交和评审,NIST在公钥加密类别中选出了一个名为CRYSTALS-Kyber的优胜者,在数字签名类别中选出了三个优胜者(数字签名用于安全地识别信息的发送者)。

NIST面向全球征集PQC标准化及第四轮入选算法
目前,NIST正与研究人员合作,将获奖算法标准化,以便程序员可以开始着手量子保密工作。
然而,令人担忧的是,包括CRYSTALS-Kyber在内的四种入选算法中,有三种是基于格数学的。甚至在2023年12月1日,网络安全公司Cryspen的研究人员揭示了两个相关漏洞,被合称为“KyberSlash”,可能导致攻击者获取加密密钥。
专家们确信这些问题很难解决,但谁也不能保证未来的突破不会破解它们。

已知最早的密码学形式之一是一种用来替换文字中字母的密码。
凯撒大帝在他的信息中,用罗马字母表中相隔三个位置的字母替换了每个字母。在英语中,这意味着“a”变成 “d”,“b”变成“e”,以此类推。
要解密凯撒的信息,只需逆向操作、将字母按字母表顺序移动三个位置即可。
凯撒的替换方案有无穷无尽的变化,上课传纸条的孩子们可以自己创造,把“a”换成心形、把“b”换成星形,等等。没收孩子纸条的老师可能会注意到纸条上有许多孤立的三角形,从而推断出三角形代表“I”或 “a”。
密码破译者通常可以通过比较不同符号与常见英文文本中字母的出现频率,来破解更复杂的替换方案。
现代密码学的黄金标准,即高级加密标准(AES),在凯撒方法的基础上进行了大幅扩展。
它通过反复替换条目和像洗扑克牌一样洗牌来扰乱信息。经过足够多的洗牌和替换后,就很难重建原始版本了。
要解密信息,就必须通过撤销每次洗牌和替换来解码。
对于一副实体扑克牌来说,这几乎是不可能的:洗牌顺序是由难以察觉的细微动作决定的。
但计算机是根据一套精确的指令来洗牌的,例如“将第二个条目移到第五个位置”,而这些指令很容易撤销:计算机只需反向执行指令即可,例如“将第五个条目移到第二个位置”。
与凯撒密码一样,AES也有对称的加密和解密程序。它向前和向后应用相同的程序,就像朝相反方向拧钥匙来锁门和开锁一样。
直到20世纪70年代,这些“对称加密技术”(也称为对称密钥加密技术)一直是唯一的加密技术。
但它有一个很大的局限性:在交换任何信息之前,发送方和接收方需要就加密和解密的程序达成一致,可以是当面交换,也可以通过可信的单独通信方式交换。
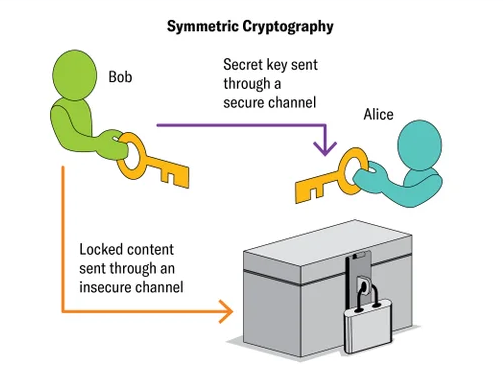

很难想象没有这种限制的对称加密技术还能有什么替代方案。
然而,1974年,加州大学伯克利分校的本科生拉尔夫·默克尔(Ralph Merkle)提出了一个课堂项目,研究“两个人在没有任何事先安排的情况下进行安全通信”的方法。
默克尔设想了一个系统,在这个系统中,两个人完全在公开场合交换信息,而且总是假定有人在监听。
通过这种公开通信,他们设法建立了一个编码和解码方案,并用它来发送秘密信息。
即便有其他人在阅读这些信息,他们也无法弄清这个方案。然而,当时默克尔的提议被一位专家以“不切实际的工作假设”为由否决了。
然而,令人惊讶的是,仅仅几年后,几篇数学论文实现了默克尔的设想。
其中两种算法被称为Diffie-Hellman算法和RSA算法(Rivest-Shamir-Adleman的缩写,即算法创造者的姓氏)的算法在现代通信中无处不在。
事实证明,甚至在默克尔的课堂项目之前,英国情报组织的研究人员就已经发现了这种编码方法:公钥密码学,并将其保密。
可以这样来理解这一概念:
当您在网上查询银行账户时,您的电脑和银行服务器之间正在交换信息:您发送密码,银行发送余额。
当这些信息在互联网上移动时,其他人可能会读取这些信息。因此,这些信息需要加密。
大多数信息都是用对称加密技术(如AES)加密的,这种加密技术可以快速有效地扰乱信息。
但首先你的计算机和通信服务器需要就具体的加扰程序达成一致。
他们不能简单地把它写下来,因为他们的所有通信都可能被窃听者捕获:它们需要使用公钥加密技术。
为了理解这个过程是如何进行的,让我们想象一下,爱丽丝(Alice)和鲍勃(Bob)这两个朋友开了一家面包店,拥有一份绝密的巧克力蛋糕配方。
这个配方非常秘密,甚至连爱丽丝和鲍勃都不知道完整的配方。
他们各自添加了一种只有添加者自己知道的特殊配料。
为了制作巧克力蛋糕,爱丽丝和鲍勃交换着开始制作。
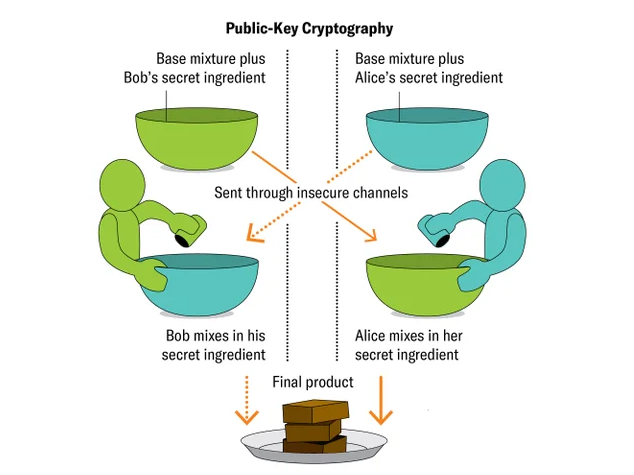
爱丽丝和鲍勃最后总能做出同样的巧克力蛋糕,但他们从不与任何人分享完整、准确的配料——包括彼此。
就连纵容他们的送货司机夏娃(Eve)也搞不清楚配方。
(在密码学中,交换秘密的两个人传统上被称为Alice和Bob,而潜在的“间谍”通常被称为Eve)。
夏娃无法推断出秘密配料,因为每当她运送秘密配料时,这些配料就会与所有基本配料混合在一起:不可能将它们分开。
当然,计算机不会烤布朗尼蛋糕;它们是用数字和数学来工作的。
在真正的公钥密码学中,我们的目标是最终得到一个共享的秘密数字:就像一个允许进入私人对话的临时口令。
然后,两台计算机可以继续使用对称加密技术(如AES)进行加密对话。
不同类型的公钥加密以不同的方式创建和共享临时口令。
爱丽丝和鲍勃在运输布朗尼蛋糕前将配料混合,从而向夏娃隐藏了他们的配方;实施公钥加密的人则会使用数学函数来混合秘密数字。
函数就像一台机器,可以输入数字,将其搅碎,然后吐出新的数字。
公钥密码学中使用的函数非常特殊:它们既要能轻松混合数字,又要让数字很难被混合。
即使夏娃看到了函数的输出,她也不可能猜出输入的是哪些秘密数字。
例如,RSA密码术就是基于乘法函数及其相反的因式分解。
通过乘法混合数字对计算机来说相对容易,即使数字非常大;但如果数字很大,撤销乘法或因式分解就非常困难。
因式分解是指回答这样一个问题:我要把哪些数字相乘才能得到这个数字?例如,对21进行因式分解可以得到3和7。
要解密用RSA创建的密码,就需要对一个大数字进行因式分解。
而2023年11月,一位著名研究科学家甚至表示,仅商用智能手机或Linux计算机就可用于破解RSA-2048加密。

这些说法似乎很虚假,但应该认识到,世界还没有准备好接受可以破解RSA-2048的现成系统,因为主要公司、组织和政府尚未过渡到抗量子时代安全的加密技术。

1994年,时任贝尔实验室研究科学家的应用数学家彼得·肖尔(Peter Shor)发现了一种方法,证明了量子计算机可以破解任何用RSA或Diffie-Hellman加密的代码。
通常情况下,求对数很容易,但离散对数问题是用另一种算术形式计算对数,在这种算术形式中,人们像在时钟上一样绕圈计数。
RSA、Diffie-Hellman都是基于离散对数的问题。
计算机科学家普遍认为,经典计算机无法快速找到离散对数。
但肖尔找到了在量子计算机上实现这一目标的方法。随后,他又运用类似的逻辑,证明了如何使用量子计算机快速计算大数因数。
——这些解决方案被称为肖尔算法。
肖尔并没有想象过为真正的量子计算机编程,他只是在黑板和纸上做数学题。
肖尔说:“当时,量子计算机似乎是遥不可及的未来。所以我主要是在想,这是一个非常漂亮的数学定理。”
但他的算法对公钥密码学有着重大影响:量子计算机可以用它破解目前使用的几乎所有密码系统。

经典计算机运行在被称为比特的0和1长串上,但量子计算机使用的是量子比特,它可以处于叠加状态:0和1的“奇异”组合。
通过在这两种状态之间徘徊,量子计算机能够以比经典计算机更快的速度执行某些任务。
不过,量子计算机也很“挑剔”。在算法运行时,量子比特需要保持叠加状态,但它们往往会“坍塌”成一串0和1。

时至今日,科学家们在量子计算领域仍然只能使用数量有限的量子比特进行计算,最大的成功是在量子计算机上算出的数字21。
2012年,英国布里斯托大学的研究人员借助量子计算机成功推算出21是7的3倍。
尽管许多专家认为能够破解RSA和Diffie-Hellman的量子计算机将在未来几十年内出现,但他们也承认时间线的不确定性。
对于需要在量子计算机崛起之前保护数字通信的密码学家来说,这种不确定性带来了担忧。
IBM的雷·哈里尚卡尔(Ray Harishankar)说:“每个行业都有其工作的某个方面,这对他们来说意义重大。”
“医疗保健公司需要确保他们在医学研究中使用的数据的安全,电力公司必须保护电网免受黑客攻击。如果发生了不好的事情,它们就会完全暴露。”
为了应对量子计算机的威胁,密码学家们需要提出一些非常难解的数学问题,即使在量子计算机的合理时间内也难以解决。
为此,NIST于2017年发起了一场抗量子密码学的挑战,征集可在标准计算机上广泛实施的公钥加密算法,以替代RSA和Diffie-Hellman算法。
NIST的数学家Lily Chen解释说:“人们使用的许多不同的联网系统和设备都必须互相交流这种新型密码学。”
在2017年截止日期之前,研究人员提交了82份不同的抗量子密码学提案。
在接下来的一年里,研究人员对这些算法进行了测试,然后NIST专家选出了26种算法进入下一轮。
在经过多轮筛选和测试后,NIST专家选择了一些基于格数学的算法作为最终的入围算法。
尽管这些算法有潜力应对未来的量子威胁,但研究人员也注意到其中一些存在可能被攻破的漏洞。
CRYSTALS-Kyber的作者之一、IBM公司的瓦迪姆·柳巴舍夫斯基(Vadim Lyubashevsky)说:“格是一个自然的选择。二十多年来,人们一直在以各种形式研究这个问题。”
格是重复排列的点阵。其中一个最简单的格看起来就像一个钉板:点排列在一个正方形格中。
数学家认为这种格是由两条基本线构成的:一条垂直线和一条等长的水平线。
想象一下,在一张纸的中心画一个点,从中心向外画一系列等长的垂直线或水平线,并标出线链的终点。
如果对所有可能的线链重复这些步骤,这些点就会形成一个正方形格,不同的初始线段会形成不同的格。
两条线的长度可能不相等,或者它们不是完全水平或垂直,而是倾斜一定角度。
绘制这样的线条链仍会产生重复的点阵,但行列会发生偏移或高度不同。
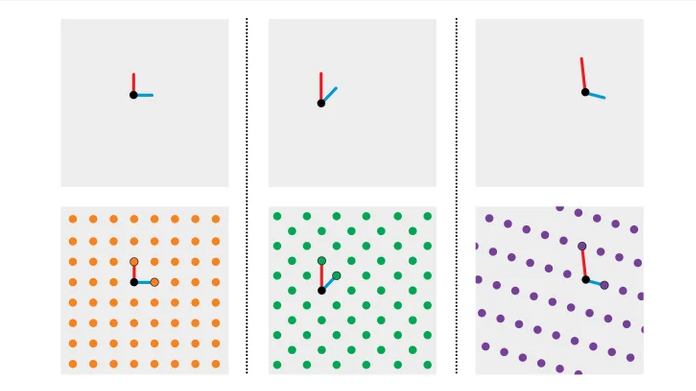
格是一些具有欺骗性的棘手数学问题的背景。
假设我在一张纸上画了两条线,并告诉你这两条线是格的组成部分。然后我在纸上某处画一个点。你能找出离那个点最近的点阵点吗?
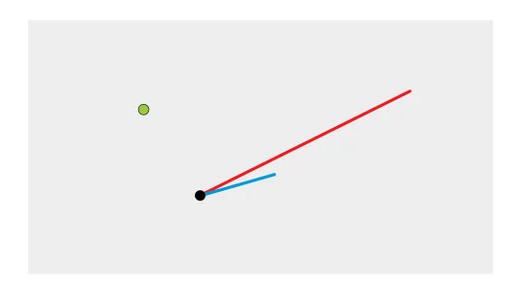
这个问题看似简单,但实际上它牵扯到一种称为“最近点问题”的复杂数学概念。
在格的背景下,即使表面上只有两条线,实际上会有许多点构成的离散格结构。
我们的视觉想象力一般仅限于三维空间,但数学家却可以描述数百维的格。
在这些高维格中,寻找最近的格点变得异常困难。
研究人员利用这种巨大的高维格来构建密码系统。例如,从一个1000维的格开始。
在这个格中选择一个点,其精确位置代表着秘密信息。
然后,可以从这个点开始微调,逐渐漂离格,进入更广阔的环境空间。
在不泄露秘密点位置的情况下,可以公开分享新位置:寻找附近的格点是一道非常艰巨的数学题。
计算机科学家已经研究这类问题数十年,他们有理由相信这些问题极具挑战性。
并且,没有人能保证基于格的加密技术永远安全。
为了防止数学上的突破解决根本问题并破解密码,密码学家需要使用各种类型的算法。
但在NIST流程的四种入围算法中,有三种是基于格的算法;在通用公钥加密类别中,唯一入选标准化的是 CRYSTALS-Kyber。

如此严重依赖单一类型的数学问题是有风险的,因为没人能够保证数学家最终不会找到破解的方法。
这种方法也未给用户提供足够的灵活性,因为结果可能是另一种类型的加密技术更适合满足他们特定需求。
即使是已经选定的标准化算法,也需要不断调整。
在第一轮提交后,研究人员发现CRYSTALS-Kyber有一个小问题,但幸运的是,作者解决了这个问题。
CRYSTALS-Kyber的创建者之一、德国马克斯-普朗克安全与隐私研究所的彼得·施瓦贝(Peter Schwabe)表示:“我们改变了参数,以获得更多比特的安全性。”
SIKE也是NIST在2022年选择的四种可能采用的算法之一,然而,令网络安全界震惊的是,比利时的一对数学家在当年7月使用一台有九年历史的非量子个人电脑,仅用了10分钟就成功破解了SIKE方案。

托马斯·德克鲁(Thomas Decru),赢得SIKE密码挑战赛的两位数学家之
破解SIKE为两位科学家赢得了微软5万美元的奖励。
然而,一旦他们宣布了这一发现,其他研究小组很快找到了更快的解密方法。
不过,这并不是NIST第一个失败的未来主义算法。
早在五个月前,位于瑞士苏黎世IBM研究所的博士后研究员沃德·比伦斯(Ward Beullens)在一个周末破解了另一种基于不同数学方法的候选算法,这种算法被称为“彩虹”(Rainbow)。
当然,提出“彩虹”算法的团队也很快对漏洞进行了修复。
2023年8月底,NIST公布了剩余三种算法的标准草案,并邀请公众发表意见。
此外,NIST还计划在2024年发布数字签名算法Falcon的标准草案,并计划在2024年的某个时候最终确定这些标准。
除了NIST之外,还有其他组织在制定密码学标准。
例如,德国联邦信息安全办公室也提供了关于使用哪些系统的建议。
其中包括两个未被NIST最终采纳的标准:一个是FrodoKEM,这是一种基于网格的密钥封装方案;另一个是Classic McEliece,它使用难以逆转的纠错码。
这两种方案都被认为比NIST的建议更安全,但它们涉及的密钥更长,因此使用起来更慢。
其他标准组织也有可能参与其中,例如互联网工程任务组(Internet Engineering Task Force),虽然它不推荐特定的加密标准,但对采用这些标准的协议有发言权。
2018年至2019年期间,中国密码研究会举办了自己的新算法竞赛。参赛作品涉及的数学问题族与NIST提案中的问题族相同,选出的优胜者是基于结构格(structured lattice)的算法。
最终,必须有一小套国际公认的标准。原因很简单,当你想进行互联网通信时,两端需要使用相同的加密技术。
大型国际公司也将发挥作用。例如,谷歌在8月份宣布将把Kyber纳入其Chrome浏览器。
这意味着如果与谷歌对话,每个人都需要使用Kyber,无论他们身在何处。
实施NIST标准并将其或类似方法推广到世界各地的计算机系统需要时间。与此同时,密码学家将继续努力开发算法,并尝试破解已有的算法。
当前的威胁是,数据可能被收集,并在稍后的阶段被解密。这也意味着世界越早采用后量子加密技术越好,因为我们无法确定20、30或40年后是否会出现量子计算机。
所以,这个问题是迫在眉睫的,我们没有时间可以浪费。
参考链接:
[1]https://www.quantum-industries.eu/insights/cloud-security-alliance-csa-countdown-clock
[2]https://www.scientificamerican.com/article/tomorrows-quantum-computers-threaten-todays-secrets-heres-how-to-protect-them/
[3]https://www.forbes.com/sites/forbestechcouncil/2024/01/19/quantum-compliance-harnessing-quantum-computing-for-enhanced-security-and-privacy/?sh=4bedaf6d7001
[4]https://www.forbes.com/sites/nokia-industry-40/2024/01/19/digitalization-undone-dont-let-quantum-threats-undermine-your-transformation-strategy/?sh=32705c8ce994
[5]https://www.forbes.com/sites/forbestechcouncil/2023/12/07/navigating-the-quantum-era-the-shift-to-quantum-safe-cryptography/?sh=382bbd035601
[6]https://www.bankinfosecurity.com/blogs/researcher-claims-to-crack-rsa-2048-quantum-computer-p-3536
[7]https://www.tomshardware.com/software/security-software/quantum-rsa-2048-encryption-cracking-breakthrough-claim-met-with-scepticism
[8]https://www.bankinfosecurity.com/blogs/researcher-claims-to-crack-rsa-2048-quantum-computer-p-3536
[9]https://www.nature.com/articles/d41586-023-03336-4
[10]https://securityaffairs.com/157740/security/quantum-computing.html
声明:本文来自光子盒,版权归作者所有。文章内容仅代表作者独立观点,不代表安全内参立场,转载目的在于传递更多信息。如有侵权,请联系 anquanneican@163.com。
