引言

今天为大家介绍一篇清华大学计算机系徐恪老师团队发表在USENIX Security 2024的工作“Defending Against Data Reconstruction Attacks in Federated Learning: An Information Theory Approach”。文章首次明确地建立了深度神经网络中的信息量化模型，为分析深度神经网络中的内部信息提供了理论工具。

Defending Against Data Reconstruction Attacks in Federated Learning: An Information Theory Approach

Qi Tan, Qi Li, Yi Zhao, Zhuotao Liu, Xiaobing Guo, and Ke Xu

文章链接：

https://www.usenix.org/system/files/sec24summer-prepub-854-tan.pdf

在AI技术的发展中，高维复杂的深度神经网络一直被人们当作黑盒模型，用以处理各类复杂的实际任务。随着AI技术进入深度学习甚至是大模型时代，深度神经网络模型逐渐成为学术界和工业界的主流，其隐私安全性也随之变得愈发重要。

保护深度神经网络隐私安全的目标是限制深度神经网络中的数据信息含量，而限制深度神经网络中数据信息含量的关键科学问题是深度神经网络中的信息量化，为此我们需要建立深度神经网络模型参数到信息含量的映射关系，以实现信息含量可计算、可比较、可调节的目的。徐恪老师团队的工作利用互信息实现了深度神经网络中的信息量化，为定量认识深度神经网络中的隐私泄露风险提供了理论工具。

01

研究背景

当前的联邦学习算法通过共享模型参数的方式进行模型训练，缓解了直接传输原始数据带来的隐私泄露风险。但是，仅共享模型参数仍然会泄露训练数据的隐私，攻击者可以通过模型参数推断特定数据是否属于训练数据集甚至可以根据这些模型参数重构原始训练数据。已有的研究希望通过差分隐私的方法定量地认识并调节隐私泄露风险，但是差分隐私主要针对的是差分攻击，无法量化数据重构引起的隐私泄露风险。有研究表明，在相同的差分隐私威胁下，根据被攻击对象选择超参数的不同，攻击者可以实现完全不同的数据重构效果。为了解决数据重构威胁下的隐私泄露风险量化问题，我们利用互信息对联邦学习中的数据隐私信息进行分析，建立了模型参数统计信息、加入噪声到数据隐私信息上界的映射关系。基于该映射关系，可以在参数统计信息和噪声给定的情况下定量地表示隐私泄露风险，也可以在参数统计信息一定的情况下，通过设定特定的隐私泄露阈值来求解加入的噪声，实现隐私泄露风险量化调节的目的。

02

进入深度神经网络中的信息与隐私泄露风险有什么关系？

深度神经网络模型在训练过程中会逐渐积累与训练数据相关的信息，而这种信息的积累会增加潜在攻击者重构原始训练数据的能力，从而加剧隐私泄露风险。这种隐私泄露风险与模型内信息含量之间的关系可以形式化为如下定理：

在定理中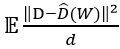，是重构训练数据与真实训练数据之间的均方距离，代表了通过深度神经网络的模型参数重构数据的精确程度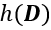； 代表训练数据集的微分熵，也表示了训练数据集的复杂程度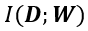；代表互信息，表示模型参数中蕴含的训练数据信息。

从定理中可以看出，通过模型参数重构原始训练数据的精确度与两个量有关：一是数据集的复杂程度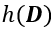。该变量越大数据重构越不精确，表明越复杂的训练数据集越难被重构；二是模型参数中蕴含的训练数据信息 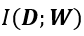。该变量越大，训练数据的重构越精确，表明进入深度神经网络的训练数据信息越多，训练数据集越容易被重构，这与我们的直观认识相符合。由于训练数据集通常是固定的，因此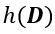是一个常数，隐私泄露风险与进入深度神经网络中的训练数据信息 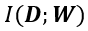密切相关。

03

信息如何进入神经网络？

在深度神经网络的训练过程中，训练数据信息会不断地进入模型。每一次与训练数据的交互都会增加模型参数中含有的训练数据信息，因此我们将模型的优化过程构建为如下的信息流动过程：

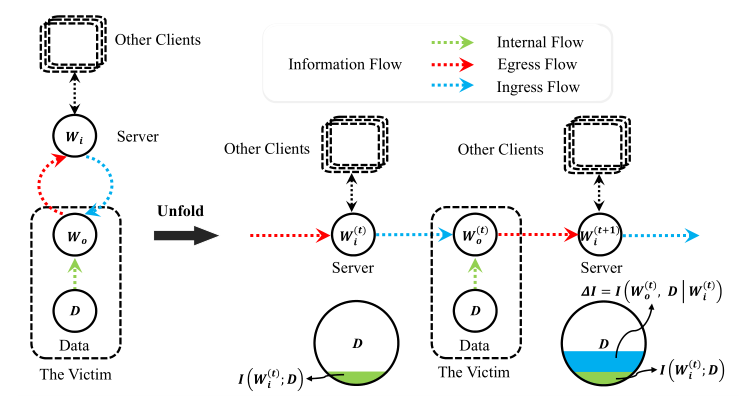
可以看到，每一次利用训练数据进行优化时，模型参数中蕴含的数据信息都会增加。利用信息论中互信息的链式法则，我们将模型训练过程中互信息的变化形式化为如下形式：

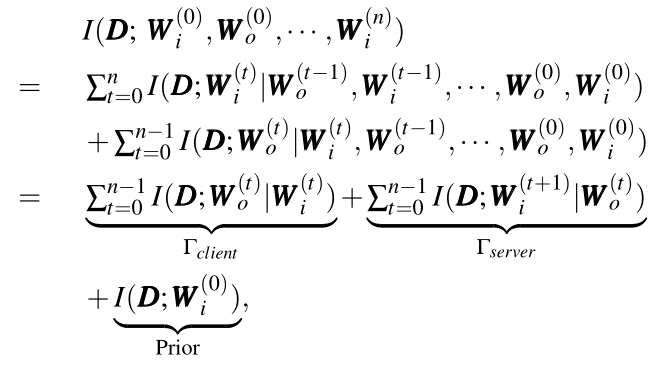
根据互信息的拆解结果，模型参数与训练数据之间的互信息可以拆解为三个部分：本地训练过程造成的隐私信息泄露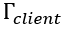，在服务器端产生的信息增量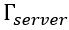以及在训练前具有的先验信息Prior。在这三个量中，后两者并不是模型训练过程导致的隐私信息泄露，而是攻击者通过模型训练以外的其他方式获得的侧信道信息，无法在训练过程中进行限制和调节，因此量化信息含量的重点是本地训练过程造成的信息泄露。

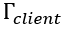为了量化在本地训练过程中进入模型的数据隐私信息，我们在深度神经网络模型中加入了高斯噪声，将其转化为含有高斯噪声的模型参数进行分析：

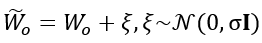
其中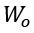，是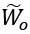的特殊情况，即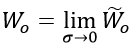。同时，根据变量之间的关系可以得到

借助信息论中高斯信道的原理（有噪高斯信道的信息传输能力有界），我们得出了以下的量化关系：

其中，是模型参数协方差矩阵的特征值， σ 代表了加入噪声的噪声规模，d 代表了模型参数的维度。

该关系说明了模型参数中增加的数据信息存储在模型参数的每一个维度中，总的信息量是每一个维度存储信息量的总和。同时，通过该关系可以在给定参数和噪声规模的情况下量化隐私泄露上限，该上限就是进入模型参数中的数据信息的最大值，从而实现了深度神经网络模型中的信息量化。

如果令，则深度神经网络模型的信息量化建立了模型参数统计量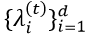、加入噪声的规模 σ 以及模型中隐私信息含量 κ 之间的关系，实现了可计算、可比较、可调节的目的。其中可计算体现在模型参数统计信息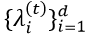（）和噪声规模 σ 给定的情况下，可以计算深度神经网络中的隐私信息含量 κ；可比较体现在经过量化后的隐私信息含量 κ 可以进行比较，从而定量地认识隐私泄露风险；可调节体现在可以根据不同的环境对 κ 进行优化调节，在给定的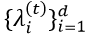下求解出 σ 的值。此时，通过加入满足高斯分布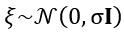的噪声，可以将参数中的隐私信息含量限制在给定值 κ 以下。结合有限的优化次数 n，在整个优化过程中的隐私信息泄露量不会超过 n·κ 。

04

实验验证

隐私泄露风险的量化调节：

当单次隐私信息泄露的阈值减小时，攻击者重构原始数据的误差明显上升。

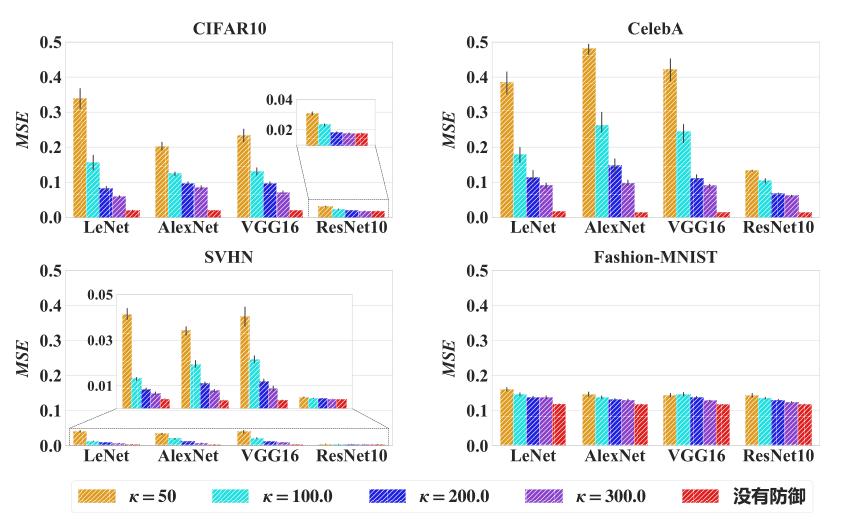
在单次隐私信息泄露的阈值给定的情况下，减小交互次数可以使攻击者重构原始数据的误差明显上升。

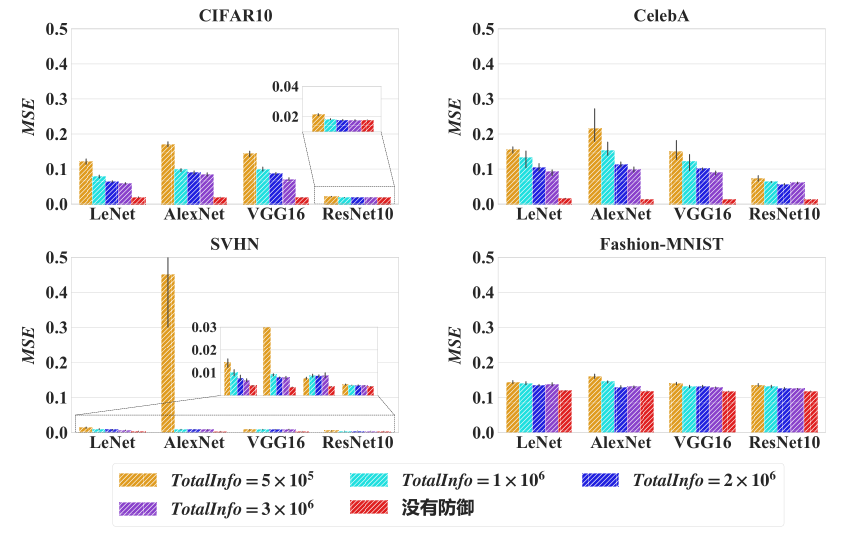
实验结果表明，通过限制单次隐私信息泄露的阈值和优化次数可以定量地调节隐私泄露的风险。

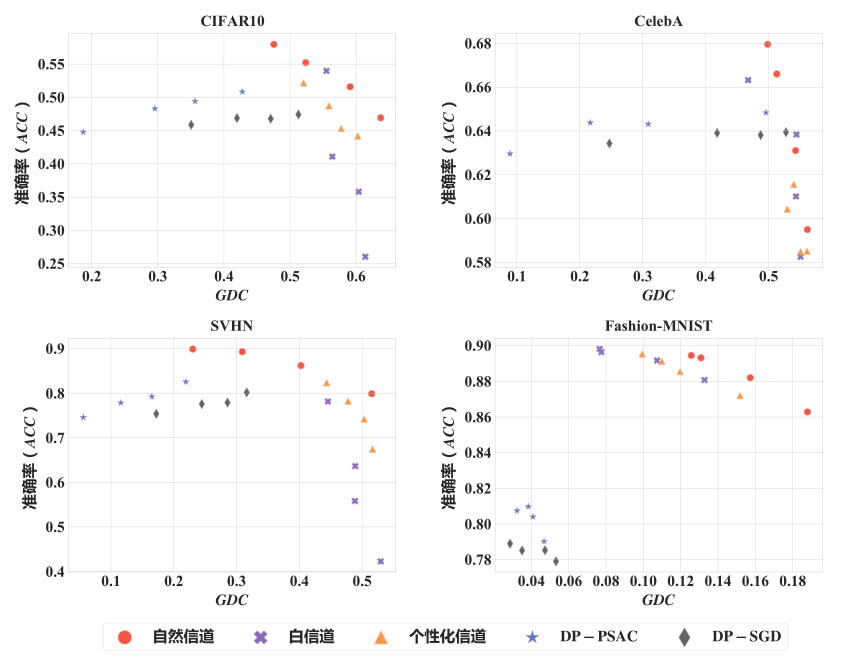
与差分隐私方法的对比：

在相同的准确率下，本工作提出的方法可以实现更好的隐私保护性能。

结语

通过量化模型参数中的数据隐私信息，我们可以定量地认识隐私泄露风险，实现隐私泄露风险可计算、可比较、可调节的目的。同时，我们还基于信息量化模型对隐私保护操作的效率进行了改进，并对差分隐私、梯度压缩等现有的隐私保护方法进行了量化分析，详细的技术细节可以查看了解：https://www.usenix.org/system/files/sec24summer-prepub-854-tan.pdf 。

声明：本文来自赛博新经济，版权归作者所有。文章内容仅代表作者独立观点，不代表安全内参立场，转载目的在于传递更多信息。如有侵权，请联系 anquanneican@163.com。